题目内容
8.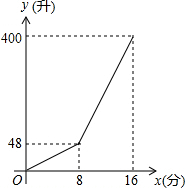 一个容积为400升的水箱,安装有A、B两个注水管,注水过程中A水管始终打开,B水管8分钟后打开,两水管的注水速度均为定值.当水箱注满时,两水管自动停止注水,注水过程中水箱中水量y(升)与A水管注水时间时间x(分)之间的函数图象如图所示.
一个容积为400升的水箱,安装有A、B两个注水管,注水过程中A水管始终打开,B水管8分钟后打开,两水管的注水速度均为定值.当水箱注满时,两水管自动停止注水,注水过程中水箱中水量y(升)与A水管注水时间时间x(分)之间的函数图象如图所示.(1)分别求A、B两水管的注水速度.
(2)当8≤x≤16时,求y与x之间的函数关系式.
(3)当两水管的注水量相同时,直接写出x的值.
分析 (1)根据题意即可得到结论;
(2)设y与x之间的函数关系式y=kx+b,解方程组即可得到结论;
(3)设x分钟两水管的注水量相同,根据题意列方程即可得到结论.
解答 解:(1)A水管的注水速度为:48÷8=6(升/分),
∵(400-48)÷(16-8)=44,
∴B水管的注水速度为:44-6=38(升/分);
(2)当8≤x≤16时,设y与x之间的函数关系式y=kx+b,
把点(8,48),(16,400)代入得$\left\{\begin{array}{l}{8k+b=48}\\{16k+b=400}\end{array}\right.$,解得:$\left\{\begin{array}{l}{k=44}\\{b=-304}\end{array}\right.$,
∴y与x之间的函数关系式y=44x-304;
(3)设x分钟两水管的注水量相同,
根据题意得6x=38(x-8),
解得x=9.5,
答:当两水管的注水量相同时,x的值是9.5.
点评 本题考查了一次函数的应用,主要考查学生分析问题和解决问题的能力,题目比较好,但是有一定的难度.

练习册系列答案
相关题目
6.如图图形中,由∠1=∠2能得到AB∥CD的是( )
| A. | 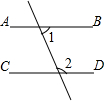 | B. |  | ||
| C. | 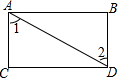 | D. | 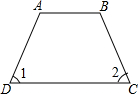 |
19.若${({2+y})^2}+\sqrt{x+y-1}=0$,则xy的值等于( )
| A. | -6 | B. | -2 | C. | 2 | D. | 6 |
13.一个正方形的面积为2,则它的边长是( )
| A. | 4 | B. | ±$\sqrt{2}$ | C. | -$\sqrt{2}$ | D. | $\sqrt{2}$ |
18.∠α的余角为65°,则∠α的度数为( )
| A. | 35° | B. | 25° | C. | 45° | D. | 65° |
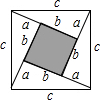 如图正方形的面积可以用两种方法得出:即c2或(b-a)2+4×$\frac{1}{2}ab$,由此可推出a2+b2=c2,若直角三角形中两直角边的和a+b=4,斜边c长为3,利用该等式来计算直角三角形的面积是$\frac{7}{4}$.
如图正方形的面积可以用两种方法得出:即c2或(b-a)2+4×$\frac{1}{2}ab$,由此可推出a2+b2=c2,若直角三角形中两直角边的和a+b=4,斜边c长为3,利用该等式来计算直角三角形的面积是$\frac{7}{4}$.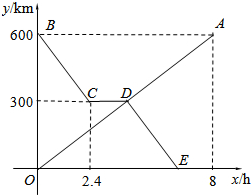 货车和轿车分别从甲、乙两地同时出发,沿同一公路相向而行.轿车出发2.4h后休息,直至与货车相遇后,以原速度继续行驶.设货车出发xh后,货车、轿车分别到达离甲地y1km和y2km的地方,图中的线段OA、折线BCDE分别表示y1、y2与x之间的函数关系.
货车和轿车分别从甲、乙两地同时出发,沿同一公路相向而行.轿车出发2.4h后休息,直至与货车相遇后,以原速度继续行驶.设货车出发xh后,货车、轿车分别到达离甲地y1km和y2km的地方,图中的线段OA、折线BCDE分别表示y1、y2与x之间的函数关系.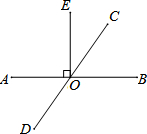 如图,直线AB、CD相交于点O,EO⊥AB,垂足为O,∠EOC:∠AOD=7:11,求∠DOE的度数.
如图,直线AB、CD相交于点O,EO⊥AB,垂足为O,∠EOC:∠AOD=7:11,求∠DOE的度数.