题目内容
5.如图是一个长为2a,宽为2b的长方形,沿图中虚线剪开,可分成四块小长方形.(1)求出图1的长方形面积;
(2)将四块小长方形拼成一个图2的正方形,利用阴影部分面积的不同表示方法,直接写出代数式(a+b)2、(a-b)2、ab之间的等量关系.
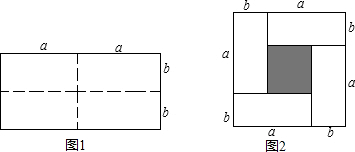
分析 (1)由长方形面积=长×宽得出;
(2)根据图形可知:大正方形是由四个小长方形和中间阴影的小正方形组成,且小正方形的边长为a-b,列式即可得出结论.
解答 解:(1)S=2a•2b=4ab,
则图1的长方形的面积为4ab;
(2)由S大正方形=4S小长方形+S阴影得:
(a+b)2=4ab+(a-b)2.
点评 本题考查了对完全平方公式几何意义的理解,本题是代数与几何图形的有机结合,利用几何图形的面积来导出完全平方公式,根据组合图形的各部分图形面积公式,和或差得出.

练习册系列答案
相关题目
3. 甲、乙两车从A城出发前往B城,在整个行驶过程中,汽车离开A城的距离y(km)与行驶时间t(h)的函数图象如图所示,下列说法正确的有( )
甲、乙两车从A城出发前往B城,在整个行驶过程中,汽车离开A城的距离y(km)与行驶时间t(h)的函数图象如图所示,下列说法正确的有( )
①甲车的速度为50km/h ②乙车用了3h到达B城
③甲车出发4h时,乙车追上甲车 ④乙车出发后经过1h或3h两车相距50km.
 甲、乙两车从A城出发前往B城,在整个行驶过程中,汽车离开A城的距离y(km)与行驶时间t(h)的函数图象如图所示,下列说法正确的有( )
甲、乙两车从A城出发前往B城,在整个行驶过程中,汽车离开A城的距离y(km)与行驶时间t(h)的函数图象如图所示,下列说法正确的有( )①甲车的速度为50km/h ②乙车用了3h到达B城
③甲车出发4h时,乙车追上甲车 ④乙车出发后经过1h或3h两车相距50km.
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
13.一个正方形的面积为2,则它的边长是( )
| A. | 4 | B. | ±$\sqrt{2}$ | C. | -$\sqrt{2}$ | D. | $\sqrt{2}$ |
15.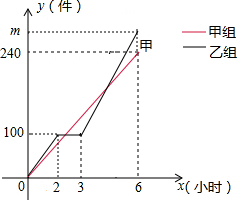 甲、乙两组工人同时加工某种零件,乙组在工作中有一次停产更换设备,之后乙组的工作效率是原来的1.2倍,甲、乙两组加工出的零件合在一起装箱,每200件装一箱,零件装箱的时间忽略不计,两组各自加工零件的数量y(件)与时间x(时)的函数图象如图,以下说法错误的是( )
甲、乙两组工人同时加工某种零件,乙组在工作中有一次停产更换设备,之后乙组的工作效率是原来的1.2倍,甲、乙两组加工出的零件合在一起装箱,每200件装一箱,零件装箱的时间忽略不计,两组各自加工零件的数量y(件)与时间x(时)的函数图象如图,以下说法错误的是( )
 甲、乙两组工人同时加工某种零件,乙组在工作中有一次停产更换设备,之后乙组的工作效率是原来的1.2倍,甲、乙两组加工出的零件合在一起装箱,每200件装一箱,零件装箱的时间忽略不计,两组各自加工零件的数量y(件)与时间x(时)的函数图象如图,以下说法错误的是( )
甲、乙两组工人同时加工某种零件,乙组在工作中有一次停产更换设备,之后乙组的工作效率是原来的1.2倍,甲、乙两组加工出的零件合在一起装箱,每200件装一箱,零件装箱的时间忽略不计,两组各自加工零件的数量y(件)与时间x(时)的函数图象如图,以下说法错误的是( )| A. | 甲组加工零件数量y与时间x的关系式为y甲=40x | |
| B. | 乙组加工零件总量m=280 | |
| C. | 经过2$\frac{1}{2}$小时恰好装满第1箱 | |
| D. | 经过4$\frac{3}{4}$小时恰好装满第2箱 |
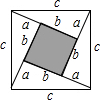 如图正方形的面积可以用两种方法得出:即c2或(b-a)2+4×$\frac{1}{2}ab$,由此可推出a2+b2=c2,若直角三角形中两直角边的和a+b=4,斜边c长为3,利用该等式来计算直角三角形的面积是$\frac{7}{4}$.
如图正方形的面积可以用两种方法得出:即c2或(b-a)2+4×$\frac{1}{2}ab$,由此可推出a2+b2=c2,若直角三角形中两直角边的和a+b=4,斜边c长为3,利用该等式来计算直角三角形的面积是$\frac{7}{4}$.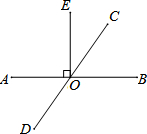 如图,直线AB、CD相交于点O,EO⊥AB,垂足为O,∠EOC:∠AOD=7:11,求∠DOE的度数.
如图,直线AB、CD相交于点O,EO⊥AB,垂足为O,∠EOC:∠AOD=7:11,求∠DOE的度数.