题目内容
4.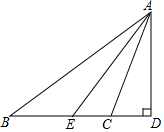 如图所示,△ABC中,∠B=36°,∠ACB=110°,AE是∠BAC的平分线.
如图所示,△ABC中,∠B=36°,∠ACB=110°,AE是∠BAC的平分线.(1)求∠AEC的度数;
(2)过△ABC的顶点A作BC边上的高AD.求∠DAE的度数.
分析 (1)根据三角形的内角和定理,可得∠BAC,根据角平分线的定义,可得∠BAE的度数,根据外角的性质,可得∠DEA,根据直角三角形的性质,可得答案;
(2)由垂直的定义得到∠D=90°,根据三角形的内角和即可得到结论.
解答 解:(1)∵∠BAC=180°-∠B-∠ACB=180°-36°-110°=34°.
∵AE是∠BAC的平分线,
∴∠BAE=$\frac{1}{2}$∠BAC=17°.
∴∠AEC=∠B+∠BAE=36°+17°=53°;
(2)∵AD⊥BD,
∴∠D=90°,
∴∠DAE=90°-53°=37°.
点评 本题考查了三角形内角和定理,利用了三角形内角和定理,三角形外角的性质,直角三角形的性质.

练习册系列答案
相关题目
 如图,已知AB∥CD,∠EAF=$\frac{1}{4}$∠EAB,∠ECF=$\frac{1}{4}$∠ECD,求证:∠AFC=$\frac{3}{4}$∠AEC.
如图,已知AB∥CD,∠EAF=$\frac{1}{4}$∠EAB,∠ECF=$\frac{1}{4}$∠ECD,求证:∠AFC=$\frac{3}{4}$∠AEC.
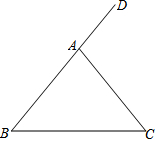 如图,在△ABC中,AB=AC,∠DAC是△ABC的一个外角.
如图,在△ABC中,AB=AC,∠DAC是△ABC的一个外角.