��Ŀ����
��ͼ����ƽ��ֱ������ϵ�У�������y=﹣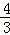 x2+bx+c��x�ύ��A��D���㣬��y�ύ�ڵ�B���ı���OBCD�Ǿ��Σ���A������Ϊ��1��0������B������Ϊ��0��4������֪��E��m��0�����߶�DO�ϵĶ��㣬����E��PE��x�ύ�������ڵ�P����BC�ڵ�G����BD�ڵ�H��
x2+bx+c��x�ύ��A��D���㣬��y�ύ�ڵ�B���ı���OBCD�Ǿ��Σ���A������Ϊ��1��0������B������Ϊ��0��4������֪��E��m��0�����߶�DO�ϵĶ��㣬����E��PE��x�ύ�������ڵ�P����BC�ڵ�G����BD�ڵ�H��
��1����������ߵĽ���ʽ��
��2������P��ֱ��BC�Ϸ�ʱ�����ú�m�Ĵ���ʽ��ʾPG�ij��ȣ�
��3���ڣ�2���������£��Ƿ���������ĵ�P��ʹ����P��B��GΪ��������������DEH���ƣ������ڣ������ʱm��ֵ���������ڣ���˵�����ɣ�
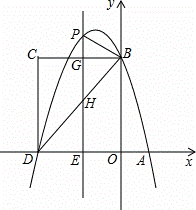
��
�⣺��1����������y=﹣ x2+bx+c��x�ύ�ڵ�A��1��0������y�ύ�ڵ�B��0��4����
x2+bx+c��x�ύ�ڵ�A��1��0������y�ύ�ڵ�B��0��4����
�� �����
����� ��
��
�������ߵĽ���ʽΪy=﹣ x2﹣
x2﹣ x+4��
x+4��
��2����E��m��0����B��0��4����PE��x�ύ�������ڵ�P����BC�ڵ�G��
��P��m��﹣ m2﹣
m2﹣ m+4����G��m��4����
m+4����G��m��4����
��PG=﹣ m2﹣
m2﹣ m+4﹣4=﹣
m+4﹣4=﹣ m2﹣
m2﹣ m��
m��
��P��ֱ��BC�Ϸ�ʱ������Ҫ�����������ֱ��BC�Ľ��㣬
��4=﹣ m2﹣
m2﹣ m+4�����m=﹣2��0��
m+4�����m=﹣2��0��
��m��ȡֵ��Χ��﹣2��m��0��
PG�ij���Ϊ��﹣ m2﹣
m2﹣ m��﹣2��m��0����
m��﹣2��m��0����
��3���ڣ�2���������£����ڵ�P��ʹ����P��B��GΪ��������������DEH���ƣ�
��y=﹣ x2﹣
x2﹣ x+4��
x+4��
�൱y=0ʱ��﹣ x2﹣
x2﹣ x+4=0��
x+4=0��
���x=1��﹣3��
��D��﹣3��0����
����P��ֱ��BC�Ϸ�ʱ��﹣2��m��0��
��ֱ��BD�Ľ���ʽΪy=kx+4��
��D��﹣3��0�����룬��﹣3k+4=0��
���k= ��
��
��ֱ��BD�Ľ���ʽΪy= x+4��
x+4��
��H��m�� m+4����
m+4����
�����������
�������BGP�ס�DEH����ô =
= ��
��
�� =
= ��
��
���m=﹣3��﹣1��
��﹣2��m��0����m=﹣1��
�������PGB�ס�DEH����ô =
= ��
��
�� =
= ��
��
��﹣2��m��0�����m=﹣ ��
��
�����������ڣ�2���������£����ڵ�P��ʹ����P��B��GΪ��������������DEH���ƣ���ʱm��ֵΪ﹣1��﹣ ��
��


��


 ��E��AC�ڵ�E��
��E��AC�ڵ�E�� ��BP��=5
��BP��=5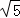 ʱ�����߶�AB�ij���
ʱ�����߶�AB�ij���

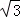 ������ABC�Ƶ�P��ת180�㣬�õ���MCB��
������ABC�Ƶ�P��ת180�㣬�õ���MCB��