题目内容
 如图,P是⊙O的直径AB的延长线上一点,PC是⊙O的切线,C为切点,PM平分∠APC交AC于点M,tanA=
如图,P是⊙O的直径AB的延长线上一点,PC是⊙O的切线,C为切点,PM平分∠APC交AC于点M,tanA=| 1 |
| 2 |
考点:切线的性质
专题:计算题
分析:连结OC,连结BC交PM于N,作CH⊥PM于H,根据圆周角定理得∠ACB=90°,利用正切的定义得tan∠A=
=
,设BC=x,则AC=2x,利用勾股定理计算出AB=
x,由于∠A+∠ABC=90°,而∠ABC=∠OCB,所以∠A+∠OCB=90°;根据切线的性质得∠3+∠OCB=90°,则由∠A=∠3,可判断△PCB∽△PAC,根据相似比得PA=2PC,PB=
PC,PC2=PB•PA,所以PC2=
PC•(
x+
PC),可计算出PC=
x;再利用三角形外角性质可证明∠1=∠2,则CM=CN;然后证明△PAM∽△PCN,根据相似比得AM=2CN,利用AM=AC-CM得2x-CN=2CN,解得CN=
x;接着判断△CHN为等腰直角三角形,则CH=
CN=
x,最后在Rt△PCH中,利用正弦的定义求解.
| BC |
| AC |
| 1 |
| 2 |
| 5 |
| 1 |
| 2 |
| 1 |
| 2 |
| 5 |
| 1 |
| 2 |
2
| ||
| 3 |
| 2 |
| 3 |
| ||
| 2 |
| ||
| 3 |
解答:解:连结OC,连结BC交PM于N,作CH⊥PM于H,如图,
∵AB为直径,
∴∠ACB=90°,
∴tan∠A=
=
,
设BC=x,AC=2x,
∴AB=
=
x,
∵∠A+∠ABC=90°,
而∠ABC=∠OCB,
∴∠A+∠OCB=90°,
∵PC是⊙O的切线,
∴OC⊥PC
∴∠3+∠OCB=90°,
∴∠A=∠3,
∴△PCB∽△PAC,
∴
=
=
=
,
∴PA=2PC,PB=
PC,PC2=PB•PA
∴PC2=
PC•(
x+
PC),
∴PC=
x,
∵∠1=∠A+∠4,∠2=∠3+∠5,
∴∠1=∠2,
∴CM=CN,
∵PM平分∠APC交AC于点M,
∴∠4=∠5,
∴△PAM∽△PCN,
∴
=
=2,
∴AM=2CN,
而AM=AC-CM,
∴2x-CN=2CN,解得CN=
x,
∵∠1=∠2,∠MCN=90°,
∴∠2=45°,
∴CH=
CN=
x,
在Rt△PCH中,sin∠CPH=
=
=
,
∴sin∠MPC=
.
∵AB为直径,

∴∠ACB=90°,
∴tan∠A=
| BC |
| AC |
| 1 |
| 2 |
设BC=x,AC=2x,
∴AB=
| AC2+BC2 |
| 5 |
∵∠A+∠ABC=90°,
而∠ABC=∠OCB,
∴∠A+∠OCB=90°,
∵PC是⊙O的切线,
∴OC⊥PC
∴∠3+∠OCB=90°,
∴∠A=∠3,
∴△PCB∽△PAC,
∴
| PB |
| PC |
| PC |
| PA |
| BC |
| AC |
| 1 |
| 2 |
∴PA=2PC,PB=
| 1 |
| 2 |
∴PC2=
| 1 |
| 2 |
| 5 |
| 1 |
| 2 |
∴PC=
2
| ||
| 3 |
∵∠1=∠A+∠4,∠2=∠3+∠5,
∴∠1=∠2,
∴CM=CN,
∵PM平分∠APC交AC于点M,
∴∠4=∠5,
∴△PAM∽△PCN,
∴
| AM |
| CN |
| PA |
| PC |
∴AM=2CN,
而AM=AC-CM,
∴2x-CN=2CN,解得CN=
| 2 |
| 3 |
∵∠1=∠2,∠MCN=90°,
∴∠2=45°,
∴CH=
| ||
| 2 |
| ||
| 3 |
在Rt△PCH中,sin∠CPH=
| CH |
| PC |
| ||||
|
| ||
| 10 |
∴sin∠MPC=
| ||
| 10 |
点评:本题考查了切线的性质:圆的切线垂直于经过切点的半径;经过圆心且垂直于切线的直线必经过切点;经过切点且垂直于切线的直线必经过圆心.也考查了相似三角形的判定与性质和圆周角定理.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案
相关题目
 如图,四个村庄A、B、C、D分别在正方形ABCD的四个顶点处,E是通往A,B村庄公路上的一所小学,且BE=2km,AE=3BE,打算在A,C村庄的公路上修一个自来水站P向B,E两地供水.请问P修在A,C村庄的公路上的什么位置,才能使PB+PE的值最小?并求出最小值.
如图,四个村庄A、B、C、D分别在正方形ABCD的四个顶点处,E是通往A,B村庄公路上的一所小学,且BE=2km,AE=3BE,打算在A,C村庄的公路上修一个自来水站P向B,E两地供水.请问P修在A,C村庄的公路上的什么位置,才能使PB+PE的值最小?并求出最小值. 几何问题:
几何问题: 如图,C是线段BD的中点,AD=3,AC=7,求线段AB的长.
如图,C是线段BD的中点,AD=3,AC=7,求线段AB的长.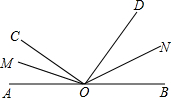 如图,∠AOB是平角,OM、ON分别是∠AOC、∠BOD的平分线. 且∠AOC=40°,∠BOD=50°.求:
如图,∠AOB是平角,OM、ON分别是∠AOC、∠BOD的平分线. 且∠AOC=40°,∠BOD=50°.求: