题目内容
如图，在△ABC中，AF=2BF，CE=3AE，CD=2BD．连接CF交DE于P点，求| EP |
| DP |
考点：平行线分线段成比例
专题：计算题
分析：连结DF，如图，由AF=2BF，CD=2BD，则
=
，所以根据平行线分线段成比例定理的逆定理得到DF∥AC，于是根据平行线分线段成比例定理得到
=
=
，所以AC=3DF，加上CE=3AE，于是可得
=
，然后根据平行线分线段成比例定理，由DF∥CE即可得到
=
=
．
| BF |
| AF |
| BD |
| CD |
| DF |
| AC |
| BD |
| BC |
| 1 |
| 3 |
| CE |
| DF |
| 9 |
| 2 |
| PE |
| PD |
| CE |
| DF |
| 9 |
| 2 |
解答：解：连结DF，如图，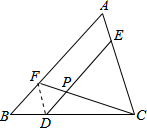
∵AF=2BF，CD=2BD，
∴
=
，
∴DF∥AC，
∴
=
=
，
∴AC=3DF，即AE+CE=3DF，
而CE=3AE，
∴
CE+CE=3DF，
∴
=
，
∵DF∥CE，
∴
=
=
．
∵AF=2BF，CD=2BD，
∴
| BF |
| AF |
| BD |
| CD |
∴DF∥AC，
∴
| DF |
| AC |
| BD |
| BC |
| 1 |
| 3 |
∴AC=3DF，即AE+CE=3DF，
而CE=3AE，
∴
| 1 |
| 3 |
∴
| CE |
| DF |
| 9 |
| 2 |
∵DF∥CE，
∴
| PE |
| PD |
| CE |
| DF |
| 9 |
| 2 |
点评：本题考查了平行线分线段成比例：三条平行线截两条直线，所得的对应线段成比例．也考查了平行线分线段成比例定理的逆定理．
练习册系列答案
相关题目
图中同旁内角有多少对？请逐一写出来．
△ABC是等腰三角形，两腰上的高BE，CD相交于点O．
如图，直线y=kx+b与y轴的交点坐标为A（0，1），与x轴的标点坐标为B（-3，0），P，Q分别是射线BO和射线BA上的动点． 
2002年8月在北京召开的国际数学家大会的会徽取材于我国古代数学家赵爽的《勾股圆方图》它是由四个全等的直角三角形和中间的一个小正方形拼成的一个大正方形，如图，若大正方形的面积是64，一个直角三角形两直角边长和为10，则小正方形的面积为
如图，Rt△ABC中，∠C=90°，O为AB上一点，以O为圆心，OB长为半径的圆，交BC边于点D，与AC边相切于点E．