题目内容
 如图,△ABC中,∠C=90°,∠B=30°,AD平分∠BAC,AB=2
如图,△ABC中,∠C=90°,∠B=30°,AD平分∠BAC,AB=2| 3 |
考点:勾股定理,角平分线的性质,含30度角的直角三角形
专题:
分析:在Rt△ABC中,∠B=30°,AB=2
,根据含30°的直角三角形三边的关系得AC=
AB=
,利用三角形内角和定理得∠BAC=60°,又因为AD平分∠BAC得到∠DAC=30°,再根据含30°的直角三角形三边的关系得DC=
AC=1,且AD=2DC,即可得到答案.
| 3 |
| 1 |
| 2 |
| 3 |
| ||
| 3 |
解答:解:在Rt△ABC中,∠B=30°,AB=2
,
∴AC=
AB=
,∠BAC=60°,
又∵AD平分∠BAC,
∴∠DAC=
∠BAC=30°,
在Rt△ACD中,∠DAC=30°,AC=
,
∴DC=
AC=1,
AD=2DC=2.
| 3 |
∴AC=
| 1 |
| 2 |
| 3 |
又∵AD平分∠BAC,
∴∠DAC=
| 1 |
| 2 |
在Rt△ACD中,∠DAC=30°,AC=
| 3 |
∴DC=
| ||
| 3 |
AD=2DC=2.
点评:此题主要考查了直角三角形的性质,关键是掌握在直角三角形中,30°角所对的直角边等于斜边的一半.

练习册系列答案
 新活力总动员暑系列答案
新活力总动员暑系列答案 龙人图书快乐假期暑假作业郑州大学出版社系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案
相关题目
 如图,点A(2,6),y轴上有一点B,使得OB=AB,求点B的坐标.
如图,点A(2,6),y轴上有一点B,使得OB=AB,求点B的坐标. 如图,AB是⊙O的直径,C、D是圆上的两点.已知BC=3,AB=5,求tan∠ADC.
如图,AB是⊙O的直径,C、D是圆上的两点.已知BC=3,AB=5,求tan∠ADC.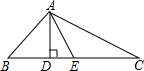 如图,△ABC中,AB=2,BC=5,AC=4.AD、AE分别为CB边上的高和中线,求DE的长.
如图,△ABC中,AB=2,BC=5,AC=4.AD、AE分别为CB边上的高和中线,求DE的长.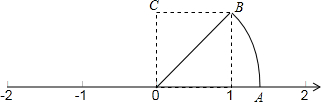 如图,四边形OEBC为正方形.
如图,四边形OEBC为正方形.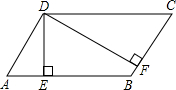 如图,已知平行四边形ABCD的周长为25cm,对边的距离分别为DE=2cm,DF=3cm,求:这个平行四边形的面积.
如图,已知平行四边形ABCD的周长为25cm,对边的距离分别为DE=2cm,DF=3cm,求:这个平行四边形的面积.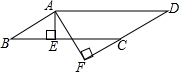 如图,在?ABCD中,AE⊥BC于点E,AF⊥CD交DC于DC的延长线于点F,AB=3cm,AF=7cm,∠EAF=30°,求∠B的度数和?ABCD周长.
如图,在?ABCD中,AE⊥BC于点E,AF⊥CD交DC于DC的延长线于点F,AB=3cm,AF=7cm,∠EAF=30°,求∠B的度数和?ABCD周长.