题目内容

18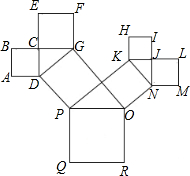．如图是一株美丽的勾股树，其中所有的四边形都是正方形，所有的三角形都是直角三角形，若正方形ABCD，正方形CEFG，正方形KHIJ，正方形JLMN的边长分别是3，5，2，3，则最大正方形ROPQ的面积是（　　）
A．13B．26C．47D．94

分析 由勾股定理得出DG2=32+52，KN2=22+32，PO2=DG2+KN2，即可得出最大正方形的面积．

解答 解：由勾股定理得：
DG2=32+52，KN2=22+32，PO2=DG2+KN2
即最大正方形E的面积为：PO2=32+52+22+32=47．
故选：C．

点评 本题考查的是勾股定理，熟知在任何一个直角三角形中，两条直角边长的平方之和一定等于斜边长的平方是解答此题的关键．

练习册系列答案
相关题目
8．关于x，y的二元一次方程组$\left\{\begin{array}{l}3x+2y=m-3\\ 2x-y=2m+1\end{array}\right.$的解互为相反数，求m的值．
9．计算：$\root{3}{-\frac{64}{125}}$+$\sqrt{1\frac{11}{25}}$-$\sqrt{16}$．
6．本学期体育老师刘老师对七（1）班50名学生进行了跳绳项目的测试，满分5分，根据测试成绩制作了下面两个统计图．

根据统计图解答下列问题：
（1）本次测试的学生中，得4分的学生有多少人？
（2）求出表示“得2分”的部分的扇形的中心角；
（3）通过一段时间的训练，刘老师对该班学生的跳绳项目进行第二次测试，测得成绩的最低分为3分，且得4分的人数没变，原来得2分的人一半得了3分，一半得了5分，试通过计算补全第二次测试的扇形统计图．
13．（1）解方程：3（x-4）=12；
（2）解方程：$\frac{2x+1}{3}$-$\frac{5x-1}{6}$=1．
3．解不等式2（x-1）≥4-3（x-3），并把解在数轴上表示出来．
10．（1）解方程：x2-2x-3=0
（2）若关于x的方程2x2-5x+c=0没有实数根，求c的取值范围．
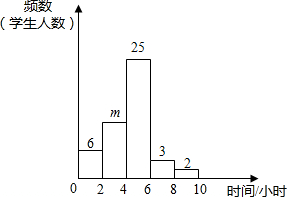7．分校为了调查初三年级学生每周的课外活动时间，随机抽查了50名初三学生，对其平均毎周参加课外活动的时间进行了调查．由调查结果绘制了频数分布直方图，根据图中信息回答下列问题：
（1）求m的值；
（2）计算50名学生的课外活动时间的平均数（每组时间用其组中值表示），对初三年级全体学生平均每周的课外活动吋问做个推断；
（3）从参加课外活动时间在6～10小时的5名学生中随机选取2人，请你用列表法，求其中至少有1人课外活动时间在8～10小时的概率．
8．下列四个命题，其中错误的命题有（　　）
①三角形的内角和与外角和相等；②四边形的内角和与外角和相等；③存在这样的一个多边形，其内角和恰是其外角和的两倍；④各边相等的多边形是正多边形．
A．1个B．2个C．3个D．4个

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网