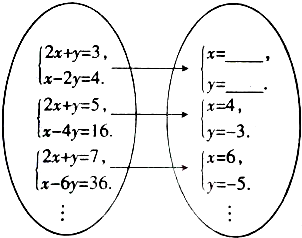
题目内容
若|ab-4|+(b-1)2=0,求
+
+…+
的值.
| 1 |
| ab |
| 1 |
| (a+3)(b+3) |
| 1 |
| (a+999)(b+999) |
考点:代数式求值,非负数的性质:绝对值,非负数的性质:偶次方
专题:
分析:首先利用绝对值的性质以及偶次方的性质得出a,b的值,再利用分数的性质化简原式求出即可.
解答:解:∵|ab-4|+(b-1)2=0,
∴b=1,a=4
+
+…+
的
=
+
+…+
=
(1-
+
-
+…+
-
)
=
(1-
)
=
.
∴b=1,a=4
| 1 |
| ab |
| 1 |
| (a+3)(b+3) |
| 1 |
| (a+999)(b+999) |
=
| 1 |
| 4 |
| 1 |
| 4×7 |
| 1 |
| 1000×1003 |
=
| 1 |
| 3 |
| 1 |
| 4 |
| 1 |
| 4 |
| 1 |
| 7 |
| 1 |
| 1000 |
| 1 |
| 1003 |
=
| 1 |
| 3 |
| 1 |
| 1003 |
=
| 334 |
| 1003 |
点评:此题主要考查了代数式求值,正确将原式变形是解题关键.

练习册系列答案
相关题目
 已知,A(n,1),B(1,-2)是一次函数y=kx+b的图象和反比例函数y=
已知,A(n,1),B(1,-2)是一次函数y=kx+b的图象和反比例函数y=