题目内容
2.在风速为24km/h的条件下,一架飞机顺风从A机场飞到B机场要用2h,它逆风飞行同样的航线要用3h,求:(1)无风时这架飞机在这一航线的航速;(2)两机场之间的航程是多少?
分析 (1)设无风时飞机的航速是x千米/时,根据顺风速度×顺风时间=逆风速度×逆风时间,列出方程求出x的值即可.
(2)由“航程=速度×时间”进行计算.
解答 解:(1)设无风时飞机的航速是x千米/时,
依题意得:2×(x+24)=3×(x-24),
解得:x=120.
答:无风时飞机的航速是120千米/时.
(2)由(1)知,无风时飞机的航速是120千米/时,则
3×(120-24)=288(千米).
答:两机场之间的航程是288千米.
点评 此题考查了一元一次方程的应用,用到的知识点是顺风速度=无风时的速度+风速,逆风速度=无风时的速度-风速,关键是根据顺风飞行的路程等于逆风飞行的路程列出方程.

练习册系列答案
 轻松暑假总复习系列答案
轻松暑假总复习系列答案
相关题目
14.下列命题,正确的是( )
| A. | 所有正方形都全等 | |
| B. | 等腰梯形的对角线互相平分 | |
| C. | 相等的圆周角所对的弧相等 | |
| D. | 顺次连结四边形各边中点所得到的四边形是平行四边形 |
1.已知5x-4y-7z=0,4x-3y-6z=0,则x:y:z为( )
| A. | 3:2:1 | B. | 9:4:1 | C. | 1:2:3 | D. | 1:4:9 |
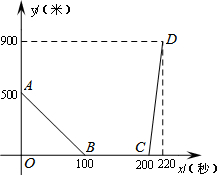 设甲、乙两车在同一直线公路上匀速行驶,开始甲车在乙车的前面,当乙车追上甲车后,两车停下来,把乙车的货物转给甲车,然后甲车继续前行,乙车向原地返回.设x秒后两车间的距离为y千米,y关于x的函数关系如图所示,
设甲、乙两车在同一直线公路上匀速行驶,开始甲车在乙车的前面,当乙车追上甲车后,两车停下来,把乙车的货物转给甲车,然后甲车继续前行,乙车向原地返回.设x秒后两车间的距离为y千米,y关于x的函数关系如图所示,
 如图,双曲线y=$\frac{k}{x}$(x>0)经过△OAB的顶点A和OB的中点C,AB∥x轴,点A的坐标为(2,3),△OAB的面积为9,则k=6.
如图,双曲线y=$\frac{k}{x}$(x>0)经过△OAB的顶点A和OB的中点C,AB∥x轴,点A的坐标为(2,3),△OAB的面积为9,则k=6.