题目内容
4. 如图,一次“台风”过后,一根旗杆被台风从离地面2.8米处吹断裂,倒下的旗杆的顶端落在离旗杆底部9.6米处,那么这根旗杆被吹断裂前有多高?(旗杆粗细、断裂磨损忽略不计)
如图,一次“台风”过后,一根旗杆被台风从离地面2.8米处吹断裂,倒下的旗杆的顶端落在离旗杆底部9.6米处,那么这根旗杆被吹断裂前有多高?(旗杆粗细、断裂磨损忽略不计)
分析 先根据勾股定理求出BC的长,再由旗杆高度=AB+BC即可解答.
解答  解:∵旗杆剩余部分、折断部分与地面正好构成直角三角形,
解:∵旗杆剩余部分、折断部分与地面正好构成直角三角形,
∴BC=$\sqrt{A{B}^{2}+A{C}^{2}}$=$\sqrt{2.{8}^{2}+9.{6}^{2}}$=10m,
∴旗杆的高=AB+BC=2.8+10=12.8m.
答:这根旗杆被吹断裂前有12.8米高.
点评 本题考查的是勾股定理在实际生活中的应用,解答此题的关键是从题中抽象出勾股定理这一数学模型,再根据勾股定理进行解答.

练习册系列答案
相关题目
15.比较二次函数y=x2与y=-x2的图象,下列结论错误的是( )
| A. | 对称轴相同 | B. | 顶点相同 | C. | 图象都有最高点 | D. | 开口方向相反 |
12.用代数式表示“a的平方的2倍与b的商”正确的是( )
| A. | 2a2÷b | B. | (2a)÷b | C. | $\frac{2{a}^{2}}{b}$ | D. | $\frac{b}{2{a}^{2}}$ |
13.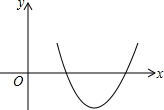 二次函数y=ax2+bx+c的图象如图所示,判断方程ax2+bx+c=0的两根,下列叙述正确的是( )
二次函数y=ax2+bx+c的图象如图所示,判断方程ax2+bx+c=0的两根,下列叙述正确的是( )
 二次函数y=ax2+bx+c的图象如图所示,判断方程ax2+bx+c=0的两根,下列叙述正确的是( )
二次函数y=ax2+bx+c的图象如图所示,判断方程ax2+bx+c=0的两根,下列叙述正确的是( )| A. | 有两个不相等的正根 | B. | 有两个相等的正根 | ||
| C. | 有一正一负两个根 | D. | 没有实数根 |
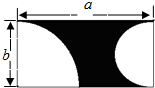 如图,长方形的长是a,宽是b,以b为半径作2个四分之一的圆.
如图,长方形的长是a,宽是b,以b为半径作2个四分之一的圆. 一个直四棱柱的俯视图如图所示,请建立适当的坐标系,在直角坐标系中作出俯视图,并标出各顶点的坐标.
一个直四棱柱的俯视图如图所示,请建立适当的坐标系,在直角坐标系中作出俯视图,并标出各顶点的坐标. 如图,在△ABC中,E是内心,延长AE交△ABC的外接圆于点D.试说明:DE=DB.
如图,在△ABC中,E是内心,延长AE交△ABC的外接圆于点D.试说明:DE=DB.