题目内容
已知C是线段AB的三等分点,D是线段AB上的点且AD=
AB,若M、N分别是CD、AB的中点,且MN=2,画图并求AB的长.
| 5 |
| 9 |
考点:两点间的距离
专题:
分析:设AB=18x,然后用x表示出相关的线段,分点C靠近A和点C靠近B两种情况列式求得x后即可求得AB的长.
解答: 解:设:AB=18x,
解:设:AB=18x,
∵AD=
AB,
∴AD=10x,
AN=
AB=9x,
∵C是线段AB的三等分点(没有明确是近A的还是近B的),
∴①若C为接近A的三等分点,
∴AC=
AB=6x,
∴CD=AD-AC=4x,
∴CM=
CD=2x,
∴AM=AC+CM=8x,
∴MN=AN-AM=x,
∴x=2,
∴AB=18x=36;
②若C为接近B的三等分点,
∴AC=
AB=12x,
∴CD=AC-AD=2x,
∴DM=
CD=x,
∴AM=AD+DM=11x,
∴MN=AM-AN=2x,
∴x=1,
∴AB=18x=18.
 解:设:AB=18x,
解:设:AB=18x,∵AD=
| 5 |
| 9 |
∴AD=10x,
AN=
| 1 |
| 2 |
∵C是线段AB的三等分点(没有明确是近A的还是近B的),
∴①若C为接近A的三等分点,
∴AC=
| 1 |
| 3 |
∴CD=AD-AC=4x,
∴CM=
| 1 |
| 2 |
∴AM=AC+CM=8x,
∴MN=AN-AM=x,
∴x=2,
∴AB=18x=36;
②若C为接近B的三等分点,
∴AC=
| 2 |
| 3 |
∴CD=AC-AD=2x,
∴DM=
| 1 |
| 2 |
∴AM=AD+DM=11x,
∴MN=AM-AN=2x,
∴x=1,
∴AB=18x=18.
点评:本题考查了两点间的距离,解题的关键是根据题意分两种情况作出图形,这是列式计算的基础.

练习册系列答案
 培优好卷单元加期末卷系列答案
培优好卷单元加期末卷系列答案
相关题目
当a<0时,|a-
|=( )
| 4a2 |
| A、a | B、-a | C、3a | D、-3a |
 如图,在△ABC中,∠B=30°,BC的垂直平分线交AB于E,垂足为D.若ED=5,则CE的长为( )
如图,在△ABC中,∠B=30°,BC的垂直平分线交AB于E,垂足为D.若ED=5,则CE的长为( )| A、7 | B、8 | C、10 | D、12 |
下列各因式分解中,结论正确的是( )
| A、x2-5x-6=(x-2)(x-3) |
| B、x2+x-6=(x+2)(x-3) |
| C、ax+ay+1=a(x+y)+1 |
| D、ma2b+mab2+ab=ab(ma+mb+1) |
有理数a、b在数轴上的位置如图所示,则把a,-a,b,-b按照从小到大的顺序排列正确的是( )


| A、-a<-b<a<b |
| B、-b<a<-a<b |
| C、-b<-a<a<b |
| D、-b<b<-a<a |
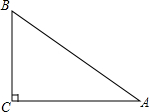 如图,原计划从A地经C地到B地修建一条高速公路,后因技术攻关,可以打隧道由A地到B地直接修建,已知高速公路每千米造价为300万元,隧道造价为每千米400万元,AC=160km,BC=120km,则改建后可省多少工程费用?
如图,原计划从A地经C地到B地修建一条高速公路,后因技术攻关,可以打隧道由A地到B地直接修建,已知高速公路每千米造价为300万元,隧道造价为每千米400万元,AC=160km,BC=120km,则改建后可省多少工程费用? 如图,已知点E在BA的延长线上,点F在AB上,∠1=∠2,∠BAC=20°,∠ACF=80°,那么FC与AD平行吗?为什么?
如图,已知点E在BA的延长线上,点F在AB上,∠1=∠2,∠BAC=20°,∠ACF=80°,那么FC与AD平行吗?为什么?