题目内容
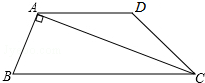 如图,在四边形ABCD中,AD∥BC,CA是∠BCD的平分线,且AB⊥AC,AB=4,AD=6,
如图,在四边形ABCD中,AD∥BC,CA是∠BCD的平分线,且AB⊥AC,AB=4,AD=6,(1)求证:三角形ADC为等腰三角形;
(2)求AC的长.
考点:勾股定理,等腰三角形的判定与性质
专题:
分析:((1)根据角平分线的定义可得,以及直线平行的性质证明∠DAC=∠DCA,再根据等角对等边可得证得;
(2)过点D作DE⊥AC于E,根据等腰三角形三线合一的性质可得AE=
AC,根据两组角对应相等的两个三角形相似求出△ABC∽△EDC,再根据相似三角形对应边成比例求出BC,然后利用勾股定理列式计算即可得解.
(2)过点D作DE⊥AC于E,根据等腰三角形三线合一的性质可得AE=
| 1 |
| 2 |
解答: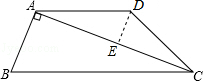 (1)证明:∵AD∥BC,
(1)证明:∵AD∥BC,
∴∠DAC=∠BCA,
又∵∠DCA=∠ACB,
∴∠DAC=∠DCA,
∴AD=CD,即△ADC是等腰三角形;
(2)解:过点D作DE⊥AC于E,则AE=CE=
AC,
∵∠1=∠2,∠BAC=∠DEC,
∴△ABC∽△EDC,
∴
=
,
即
=
,
∴BC=12,
在直角△ABC中,AC=
=
=8
.
 (1)证明:∵AD∥BC,
(1)证明:∵AD∥BC,∴∠DAC=∠BCA,
又∵∠DCA=∠ACB,
∴∠DAC=∠DCA,
∴AD=CD,即△ADC是等腰三角形;
(2)解:过点D作DE⊥AC于E,则AE=CE=
| 1 |
| 2 |
∵∠1=∠2,∠BAC=∠DEC,
∴△ABC∽△EDC,
∴
| CD |
| BC |
| CE |
| AC |
即
| 6 |
| BC |
| 1 |
| 2 |
∴BC=12,
在直角△ABC中,AC=
| BC2-AB2 |
| 122-42 |
| 2 |
点评:本题考查了相似三角形的判定与性质,平行线的性质,等腰三角形三线合一的性质,勾股定理,作辅助线构造出相似三角形并求出BC的长度是解题的关键.

练习册系列答案
 全优考典单元检测卷及归类总复习系列答案
全优考典单元检测卷及归类总复习系列答案
相关题目
下列运算正确的是( )
| A、a0=0 |
| B、(2a2)3=6a6 |
| C、(a-1)2=a2-1 |
| D、2a+3a=5a |
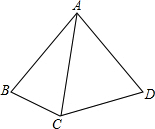 如图,AB=AC=AD,∠BAD=80°,则∠BCD的大小是
如图,AB=AC=AD,∠BAD=80°,则∠BCD的大小是 如图,⊙O是ABC的外接圆,若∠B=30°,AC=5cm,则⊙O的直径为
如图,⊙O是ABC的外接圆,若∠B=30°,AC=5cm,则⊙O的直径为