题目内容
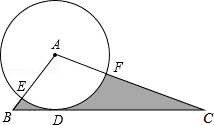 如图,在△ABC中,BC=4,以点A为圆心,2为半径的⊙A与BC相切于点D,交AB于点E,交AC于点F,且∠EAF=80°,则图中阴影部分的面积为( )
如图,在△ABC中,BC=4,以点A为圆心,2为半径的⊙A与BC相切于点D,交AB于点E,交AC于点F,且∠EAF=80°,则图中阴影部分的面积为( )| A、4 | ||
B、
| ||
C、4-
| ||
D、8-
|
考点:扇形面积的计算,切线的性质
专题:
分析:连接AD,可知AD⊥BC,结合条件可求得△ABC的面积,再求得扇形AEF的面积,根据面积的和差可求得阴影部分的面积.
解答: 解:连接AD,
解:连接AD,
∵BC为⊙A的切线,
∴AD⊥BC,
∴S△ABC=
BC•AD=
×4×2=4,
∵∠EAF=80°,
∴S扇形AEF=
=
π,
∴S阴影=S△ABC-S扇形AEF=4-
π,
故选C.
 解:连接AD,
解:连接AD,∵BC为⊙A的切线,
∴AD⊥BC,
∴S△ABC=
| 1 |
| 2 |
| 1 |
| 2 |
∵∠EAF=80°,
∴S扇形AEF=
| 80π×22 |
| 360 |
| 8 |
| 9 |
∴S阴影=S△ABC-S扇形AEF=4-
| 8 |
| 9 |
故选C.
点评:本题主要考查扇形面积的计算,掌握扇形面积公式S=
(n为圆心角的度数、r为圆的半径)是解题的关键.
| nπr2 |
| 360 |

练习册系列答案
相关题目
下列抛物线中,与y=-
x2+3x-5的开口方向大小相同,只是位置不同的是( )
| 1 |
| 2 |
A、y=-
| ||||||
| B、y=-x2+x-5 | ||||||
C、y=-
| ||||||
D、y=-
|
 如图是某超市2013年各季度“加多宝”饮料销售情况折线统计图,根据此统计图,用一句话对此超市该饮料销售情况进行简要分析:
如图是某超市2013年各季度“加多宝”饮料销售情况折线统计图,根据此统计图,用一句话对此超市该饮料销售情况进行简要分析: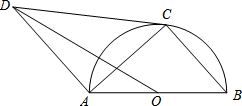 如图,AB是⊙O的直径,点C在⊙O上,CD与⊙O相切,AD∥BC,连结OD,AC.
如图,AB是⊙O的直径,点C在⊙O上,CD与⊙O相切,AD∥BC,连结OD,AC. 如图,A是反比例函数y=
如图,A是反比例函数y=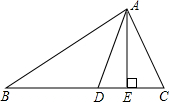 如图,AE,AD分别是△ABC的高和角平分线,且∠B=40°,∠C=60°,求∠BAD和∠DAE的度数.
如图,AE,AD分别是△ABC的高和角平分线,且∠B=40°,∠C=60°,求∠BAD和∠DAE的度数.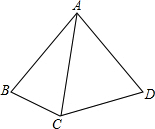 如图,AB=AC=AD,∠BAD=80°,则∠BCD的大小是
如图,AB=AC=AD,∠BAD=80°,则∠BCD的大小是