题目内容
4．计算：2cos60°-（$\sqrt{3}$-1）0+|$\sqrt{2}$-3|-（$\frac{1}{2}$）-2．分析 利用零指数幂的性质以及特殊角的三角函数值和负整数指数幂的性质、绝对值的性质分别化简求出答案．
解答 解：原式=2×$\frac{1}{2}$-1+3-$\sqrt{2}$-4
=-1-$\sqrt{2}$．
点评 此题主要考查了零指数幂的性质以及特殊角的三角函数值和负整数指数幂的性质、绝对值的性质等知识，正确化简各数是解题关键．
练习册系列答案
相关题目
14．
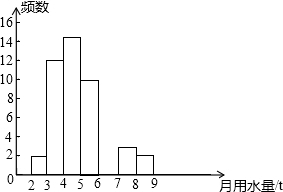小亮同学在学校组织的社会调查活动中负责了解他所居住的小区450户居民的生活用水情况，他从中随机调查了若干户居民的月均用水量（单位：t），并绘制了样本的频数分布表和频数分布直方图（如图）
（1）频数分布表中a=15，b=30%．（填百分比），c=6；补全频数分布直方图．
（2）如果家庭月均用水量“大于或等于4t且小于7t”为中等用水量家庭，请你通过样本估计总体中的中等用水量家庭大约有279户；
（3）从月均用水量在2≤x＜3，8≤x＜9这两个范围内的样本家庭中任意抽取2个，请用列表法或画树状图求抽取出的2个家庭来自不同范围的概率．
小亮同学在学校组织的社会调查活动中负责了解他所居住的小区450户居民的生活用水情况，他从中随机调查了若干户居民的月均用水量（单位：t），并绘制了样本的频数分布表和频数分布直方图（如图）| 月均用水量（单位：t） | 频数 | 百分比 |
| 2≤x＜3 | 2 | 4% |
| 3≤x＜4 | 12 | 24% |
| 4≤x＜5 | a | b |
| 5≤x＜6 | 10 | 20% |
| 6≤x＜7 | c | 12% |
| 7≤x＜8 | 3 | 6% |
| 8≤x＜9 | 2 | 4% |
（2）如果家庭月均用水量“大于或等于4t且小于7t”为中等用水量家庭，请你通过样本估计总体中的中等用水量家庭大约有279户；
（3）从月均用水量在2≤x＜3，8≤x＜9这两个范围内的样本家庭中任意抽取2个，请用列表法或画树状图求抽取出的2个家庭来自不同范围的概率．
15．
如图，直角三角板的直角顶点落在直尺边上，若∠1=56°，则∠2的度数为（ ）
如图，直角三角板的直角顶点落在直尺边上，若∠1=56°，则∠2的度数为（ ）| A． | 34° | B． | 44° | C． | 56° | D． | 28° |
12．若二次函数y=x2-6x+9的图象经过A（-1，y1），B（1，y2），C（3+$\sqrt{3}$，y3）三点．则关于y1，y2，y3大小关系正确的是（ ）
| A． | y1＞y2＞y3 | B． | y1＞y3＞y2 | C． | y2＞y1＞y3 | D． | y3＞y1＞y2 |
19．下列四组数分别是三条线段的长度，能构成三角形的是（ ）
| A． | 1，1，2 | B． | 1，3，4 | C． | 2，3，6 | D． | 4，5，8 |
9．已知△ABC∽△DEF，且周长之比为1：9，则△ABC与△DEF的高的比为（ ）
| A． | 1：3 | B． | 1：9 | C． | 1：18 | D． | 1：81 |
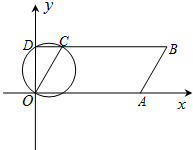如图，在平面直角坐标系中，以OC为直径的圆交y轴于点D，∠DOC=30°，OC=2．延长DC至点B，使得CB=4DC，过B点作BA∥OC交x轴于A点．
正方形ABCD边长为4，M、N分别是BC、CD上的两个动点，当M点在BC上运动时，保持AM和MN垂直，