题目内容
14.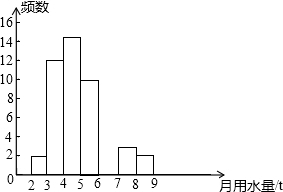 小亮同学在学校组织的社会调查活动中负责了解他所居住的小区450户居民的生活用水情况,他从中随机调查了若干户居民的月均用水量(单位:t),并绘制了样本的频数分布表和频数分布直方图(如图)
小亮同学在学校组织的社会调查活动中负责了解他所居住的小区450户居民的生活用水情况,他从中随机调查了若干户居民的月均用水量(单位:t),并绘制了样本的频数分布表和频数分布直方图(如图)| 月均用水量(单位:t) | 频数 | 百分比 |
| 2≤x<3 | 2 | 4% |
| 3≤x<4 | 12 | 24% |
| 4≤x<5 | a | b |
| 5≤x<6 | 10 | 20% |
| 6≤x<7 | c | 12% |
| 7≤x<8 | 3 | 6% |
| 8≤x<9 | 2 | 4% |
(2)如果家庭月均用水量“大于或等于4t且小于7t”为中等用水量家庭,请你通过样本估计总体中的中等用水量家庭大约有279户;
(3)从月均用水量在2≤x<3,8≤x<9这两个范围内的样本家庭中任意抽取2个,请用列表法或画树状图求抽取出的2个家庭来自不同范围的概率.
分析 (1)根据第一组的频数是2,百分比是4%即可求得总人数,然后根据百分比的意义即可求出a,b,c的值,进而可补全频数分布直方图;
(2)利用总户数540乘以对应的百分比即可求出总体中的中等用水量家庭的个数;
(3)在2≤x<3范围的两户用a、b表示,8≤x<9这两个范围内的两户用1,2表示,利用树状图法表示出所有可能的结果,然后利用概率公式求解
解答 解:(1)调查的总数是:2÷4%=50(户),
则6≤x<7部分调查的户数是:50×12%=6(户),即c=6
则4≤x<5的户数是:50-2-12-10-6-3-2=15(户),所占的百分比是:$\frac{15}{50}$×100%=30%,即a=15,b=30%,
故答案为:15.30%,6
补全频数分布直方图如图所示:
(2)中等用水量家庭大约有450×(30%+20%+12%)=279(户),
故答案为:279;
(3)在2≤x<3范围的两户用a、b表示,8≤x<9这两个范围内的两户用1,2表示.
则抽取出的2个家庭来自不同范围的概率=$\frac{8}{12}=\frac{2}{3}$.
点评 本题考查了读频数分布直方图的能力和利用统计图获取信息的能力以及求随机事件的概率;注意利用统计图获取信息时,必须认真观察、分析、研究统计图,才能作出正确的判断和解决问.

练习册系列答案
相关题目
20.某种细胞的直径是0.00000095米,将0.00000095米用科学记数法表示为( )
| A. | 9.5×10-7 | B. | 9.5×10-8 | C. | 0.95×10-7 | D. | 95×10-8 |
 [实际情境]李明家、王亮家、西山森林公园都位于石家庄市槐安路的沿线上,李明、王亮同学时分别从自己家出发,沿笔直的槐安路匀速骑行到达西山森林公园,李明的骑行速度是王亮的骑行速度的1.5倍.
[实际情境]李明家、王亮家、西山森林公园都位于石家庄市槐安路的沿线上,李明、王亮同学时分别从自己家出发,沿笔直的槐安路匀速骑行到达西山森林公园,李明的骑行速度是王亮的骑行速度的1.5倍. 如图,已知一次函数y=ax-2的图象与反比例函数y=$\frac{k}{x}$的图象交于A(k,a),B两点.
如图,已知一次函数y=ax-2的图象与反比例函数y=$\frac{k}{x}$的图象交于A(k,a),B两点.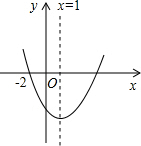 如图所示的抛物线是二次函数y=ax2+bx+c(a≠0)的图象,则下列结论:①b<0;②b+2a=0;③方程ax2+bx+c=0的两个根为x1=-2,x2=4;④a+c>b;⑤3a+c<0.其中正确的结论有( )
如图所示的抛物线是二次函数y=ax2+bx+c(a≠0)的图象,则下列结论:①b<0;②b+2a=0;③方程ax2+bx+c=0的两个根为x1=-2,x2=4;④a+c>b;⑤3a+c<0.其中正确的结论有( )