题目内容
8.用公式法解下列方程:(1)x2-2x-8=0;
(2)x2+2x-4=0;
(3)2x2-3x+2=0;
(4)3x(3x-2)+1=0;
(5)$\frac{3}{2}$x2-$\frac{1}{2}$x-1=0;
(6)x2-2$\sqrt{2}$x+2=0.
分析 (1)先计算判别式的值,然后利用求根公式解方程;
(2)先计算判别式的值,然后利用求根公式解方程;
(3)先计算根的判别式的值,然后判断方程没有实数解;
(4)先把方程化为一般式,然后利用求根公式解方程;
(5)先把方程化为整系数,然后利用求根公式解方程;
(6)先计算判别式的值,然后利用求根公式解方程.
解答 解:(1)△=(-2)2-4×1×(-8)=36,
x=$\frac{2±\sqrt{36}}{2}$,
所以x1=4,x2=-2;
(2)△=22-4×1×(-4)=20,
x=$\frac{-2±\sqrt{20}}{2}$=-1$±\sqrt{5}$,
所以x1=-1+$\sqrt{5}$,x2=-1-$\sqrt{5}$;
(3)△=(-3)2-4×2×2=-7<0,
所以方程没有实数解;
(4)9x2-6x+1=0,
△=(-6)2-4×9×1=0,
x=$\frac{6±\sqrt{0}}{2×9}$,
所以x1=x2=$\frac{1}{3}$;
(5)3x2-x-2=0,
△=12-4×3×(-2)=25,
x=$\frac{1±\sqrt{25}}{2×3}$=$\frac{1±5}{6}$,
所以x1=1,x2=-$\frac{2}{3}$;
(6)△=(-2$\sqrt{2}$)2-4×1×2=0,
x=$\frac{2\sqrt{2}±\sqrt{0}}{2×1}$=$\sqrt{2}$,
所以x1=x2=$\sqrt{2}$.
点评 本题考查了解一元二次方程-公式法:用求根公式解一元二次方程的方法是公式法.

练习册系列答案
 黄冈冠军课课练系列答案
黄冈冠军课课练系列答案
相关题目
 如图,等腰直角三角形ABC中,∠B=90°,AB=BC=8cm,动点P从A出发沿AB向B移动,通过点P引PQ∥AC,PR∥BC,问当AP等于多少时,平行四边形PQCR的面积等于16cm2?设AP的长为xcm,列出关于x的方程.
如图,等腰直角三角形ABC中,∠B=90°,AB=BC=8cm,动点P从A出发沿AB向B移动,通过点P引PQ∥AC,PR∥BC,问当AP等于多少时,平行四边形PQCR的面积等于16cm2?设AP的长为xcm,列出关于x的方程.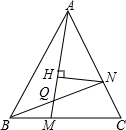 △ABC为等边三角形,点M是边BC上一点,点N是边CA上一点,且BM=CN,BN与AM相交于Q点,NH⊥AM,垂足为H.
△ABC为等边三角形,点M是边BC上一点,点N是边CA上一点,且BM=CN,BN与AM相交于Q点,NH⊥AM,垂足为H.