题目内容
13.已知抛物线C1:y=-x2+2mx+1(m为常数,且m≠0)的顶点为A,与y轴交于点C;抛物线C2与抛物线C1关于y轴对称,其顶点为B,若P是抛物线C1上的点,使得以A,B,C,P为顶点的四边形为菱形,则m的值为±$\sqrt{3}$.分析 首先假设成立,根据菱形的性质求解,求得m=±$\sqrt{3}$.
解答 解:假设抛物线C1上存在点P,使得四边形ABCP为菱形,
则PC=AB=BC,
过点A作抛物线C1的对称轴,交x轴于D,过点C作CE⊥AD于E,如图所示:
∵点A与点B关于y轴对称,点C又在y轴上,
∴AC=BC.
∴AB=BC=AC,
∴△ABC为等边三角形,
∴∠ACM=∠BCM=30°,
∵四边形ABCP为菱形,且点P在C1上,
∴点P与点C关于AD对称.
∴PC与AD的交点也为点E,
因此∠ACE=90°-30°=60°.
∵点A,C的坐标分别为A(m,m2+1),C(0,1),
∴AE=m2+1-1=m2,CE=|m|,
在Rt△ACE中,tan60°=$\frac{AE}{CE}$=$\sqrt{3}$.
∴m=±$\sqrt{3}$,
故答案为:±$\sqrt{3}$.
点评 此题考查了二次函数与四边形以及轴对称图形的综合知识;解题时要注意辅助线选择与应用,还要注意数形结合思想的应用.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
18.观察下列前三个式子:$\sqrt{{3}^{2}-1}$=$\sqrt{2}$×$\sqrt{4}$,$\sqrt{{4}^{2}-1}$=$\sqrt{3}$×$\sqrt{5}$,$\sqrt{{5}^{2}-1}$=$\sqrt{4}$×$\sqrt{6}$,…,按照这样的规律第10个式子的结果是( )
| A. | $\sqrt{9}$×$\sqrt{11}$ | B. | $\sqrt{10}$×$\sqrt{12}$ | C. | $\sqrt{11}$×$\sqrt{13}$ | D. | $\sqrt{12}$×$\sqrt{14}$ |
5.$\root{3}{(-2)^{3}}$的值是( )
| A. | -2 | B. | 2 | C. | ±2 | D. | 没有意义 |
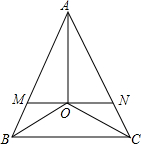 (1)如图,在△ABC中,AB=AC,∠B与∠C的角平分线交于点O,过点O作MN∥BC,分别交AB、AC于M、N,图中有几个等腰三角形?
(1)如图,在△ABC中,AB=AC,∠B与∠C的角平分线交于点O,过点O作MN∥BC,分别交AB、AC于M、N,图中有几个等腰三角形?