题目内容
18.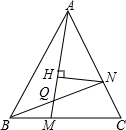 △ABC为等边三角形,点M是边BC上一点,点N是边CA上一点,且BM=CN,BN与AM相交于Q点,NH⊥AM,垂足为H.
△ABC为等边三角形,点M是边BC上一点,点N是边CA上一点,且BM=CN,BN与AM相交于Q点,NH⊥AM,垂足为H.(1)求∠AQN的度数.
(2)若BQ=3,HQ=2,求AM的长.
分析 (1)根据等边三角形的性质求得AB=BC,∠ABC=∠ACB=60°,由SAS证明△ABM≌△BCN,则∠BAM=∠NBC,利用三角形的外角和定理可得∠AQN=∠ABQ+∠BAQ,所以∠AQN=∠ABQ+∠NBM=∠ABC=60°.
(2)在Rt△NHQ中,∠AQN=60°,HQ=2,可求出QN=4,所以AM=BN=BQ+NQ=7.
解答 解:(1)∵△ABC为等边三角形,
∴∠ABC=∠ACB=60°,AB=BC,
在△ABM和△BCN中,
$\left\{\begin{array}{l}{AB=BC}\\{∠ABM=∠BCN}\\{BM=CN}\end{array}\right.$,
∴△ABM≌△BCN(SAS);
∴∠BAM=∠NBC,
∵∠AQN=∠ABQ+∠BAQ,
∴∠AQN=∠ABQ+∠NBM=∠ABC=60°;
(2)∵△ABM≌△BCN,
∴AM=BN,
∵NH⊥AM,∠AQN=60°,HQ=2,
∴QN=4,
∵BQ=3,
∴AM=BN=BQ+NQ=7.
点评 本题主要考查了全等三角形的判定与性质.利用性质和判定,学会准确地找出两个全等三角形中的对应边与对应角是关键.

练习册系列答案
 课课优能力培优100分系列答案
课课优能力培优100分系列答案 优百分课时互动系列答案
优百分课时互动系列答案
相关题目
13.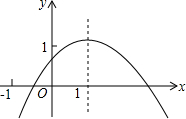 二次函数y=ax2+bx+c(a≠0)的图象如图所示,对称轴是直线x=1,则下列四个结论错误的是( )
二次函数y=ax2+bx+c(a≠0)的图象如图所示,对称轴是直线x=1,则下列四个结论错误的是( )
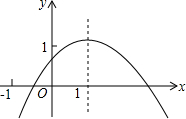 二次函数y=ax2+bx+c(a≠0)的图象如图所示,对称轴是直线x=1,则下列四个结论错误的是( )
二次函数y=ax2+bx+c(a≠0)的图象如图所示,对称轴是直线x=1,则下列四个结论错误的是( )| A. | c>0 | B. | 2a+b=0 | C. | a+b+c>0 | D. | a-b+c>0 |
 已知二次函数y=$\frac{1}{2}$x2-$\frac{3}{2}$x-2.
已知二次函数y=$\frac{1}{2}$x2-$\frac{3}{2}$x-2.