题目内容
如图：等腰直角△ABC中，若∠ACB=90°，CD=DE=CE，则∠DAB的度数为（ ）| A、60° | B、30° |
| C、45° | D、15° |
考点：等腰直角三角形
专题：
分析：根据等腰直角三角形的性质得出∠CAB=∠B=45°，根据等边三角形的性质得出∠ADC=60°，然后根据三角形外角的性质即可求得．
解答：解：∵等腰直角△ABC中，
∴∠CAB=∠B=45°，
∵CD=DE=CE，
∴△CED是等边三角形，
∴∠ADC=60°，
∵∠ADC=∠DAB+∠B，
∴∠DAB=60°-45°=15°．
故选D．
∴∠CAB=∠B=45°，
∵CD=DE=CE，
∴△CED是等边三角形，
∴∠ADC=60°，
∵∠ADC=∠DAB+∠B，
∴∠DAB=60°-45°=15°．
故选D．
点评：本题考查了等腰直角三角形的性质，等边三角形的判定和性质，三角形外角的性质，熟练掌握这些性质是解题的关键．
练习册系列答案
相关题目
已知：|a|=3，|b|=2，且|a+b|＜|a|+|b|，则a+b的值是（ ）
| A、±5 | B、±3 | C、1 | D、±1 |
如图：△PQR是等边三角形，∠APB=120°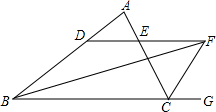
如图，∠ABC的平分线BF与△ABC中∠ACB的相邻外角∠ACG的平分线CF相交于点F，过F作DF∥BC，交AB于D，交AC于E，若BD=8cm，DE=3cm，求CE的长为在平行四边形、矩形、菱形、正方形中，对角线相等的图形有（ ）
| A、4个 | B、3个 | C、2个 | D、1个 |
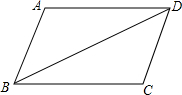如图，已知：∠ABC=∠ADC，AD∥BC．
画出如图所示物体的主视图、左视图、俯视图．
如图，在△ABC中，BD⊥AC，AB=6cm，∠A=30°，tanC=
| ||
| 2 |
A、
| ||||
B、15
| ||||
C、
| ||||
D、
|