题目内容
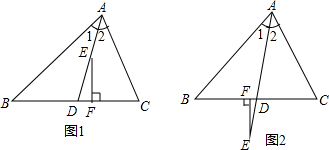
如图,在△ABC中,∠1=∠2,∠C>∠B,E为AD上一点,且EF⊥BC于F.
(1)试探索∠DEF与∠B、∠C的等量关系;
(2)如图所示,当点E在AD的延长线上时,其他条件都不变,你在(1)中探索得到的结论是否成立并说明理由.
(1)试探索∠DEF与∠B、∠C的等量关系;
(2)如图所示,当点E在AD的延长线上时,其他条件都不变,你在(1)中探索得到的结论是否成立并说明理由.

考点:三角形内角和定理,三角形的外角性质
专题:
分析:(1)过点A作AG⊥BC于点G,则EF∥AG,故∠DEF=∠DAG,根据直角三角形的性质可知∠CAG=90°-∠C,再由三角形内角和定理可知∠BAC=180°-∠B-∠C,根据∠1=∠2可知,∠2=
∠BAC=
(180°-∠B-∠C),再根据∠DAG=∠2-∠CAG即可得出结论;
(2)过点A作AH⊥BC于H,根据直角三角形两锐角互余表示出∠CAH,根据角平分线的定义可得∠2,再表示出∠DAH,然后根据三角形的内角和定理可得∠DEF=∠DAH.
| 1 |
| 2 |
| 1 |
| 2 |
(2)过点A作AH⊥BC于H,根据直角三角形两锐角互余表示出∠CAH,根据角平分线的定义可得∠2,再表示出∠DAH,然后根据三角形的内角和定理可得∠DEF=∠DAH.
解答: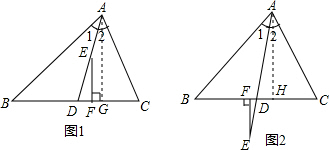 (1)解:如图1所示,过点A作AG⊥BC于点G,则EF∥AG,∠DEF=∠DAG,
(1)解:如图1所示,过点A作AG⊥BC于点G,则EF∥AG,∠DEF=∠DAG,
∵∠AGC=90°,
∴∠CAG=90°-∠C.
∵∠BAC+∠B+∠C=180°,
∴∠BAC=180°-∠B-∠C,
∵∠1=∠2,
∴∠2=
∠BAC=
(180°-∠B-∠C)=90°-
(∠B+∠C).
∵∠DAG=∠2-∠CAG=90°-
(∠B+∠C)-(90°-∠C)
=
(∠C-∠B),即∠DEF=
(∠C-∠B);
(2)解:如图2所示,过点A作AH⊥BC于H,
则∠CAH=90°-∠C,
∵∠1=∠2,
∴∠2=
(180°-∠B-∠C),
∴∠DAH=∠2-∠CAH=
(180°-∠B-∠C)-(90°-∠C)=
(∠C-∠B),
∵EF⊥BC,
∴∠DEF+∠EDF=90°,
又∵∠DAH+∠ADH=90°,∠EDF=∠ADH(对顶角相等),
∴∠DEF=∠DAH,
∴∠DEF=
(∠C-∠B).
 (1)解:如图1所示,过点A作AG⊥BC于点G,则EF∥AG,∠DEF=∠DAG,
(1)解:如图1所示,过点A作AG⊥BC于点G,则EF∥AG,∠DEF=∠DAG,∵∠AGC=90°,
∴∠CAG=90°-∠C.
∵∠BAC+∠B+∠C=180°,
∴∠BAC=180°-∠B-∠C,
∵∠1=∠2,
∴∠2=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
∵∠DAG=∠2-∠CAG=90°-
| 1 |
| 2 |
=
| 1 |
| 2 |
| 1 |
| 2 |
(2)解:如图2所示,过点A作AH⊥BC于H,
则∠CAH=90°-∠C,
∵∠1=∠2,
∴∠2=
| 1 |
| 2 |
∴∠DAH=∠2-∠CAH=
| 1 |
| 2 |
| 1 |
| 2 |
∵EF⊥BC,
∴∠DEF+∠EDF=90°,
又∵∠DAH+∠ADH=90°,∠EDF=∠ADH(对顶角相等),
∴∠DEF=∠DAH,
∴∠DEF=
| 1 |
| 2 |
点评:本题考查的是三角形内角和定理,熟知三角形内角和是180°是解答此题的关键.

练习册系列答案
相关题目
2013年中国粮食总产量达到601900000吨,数据601900000用科学记数法表示为( )
| A、60.19×107 |
| B、6.019×108 |
| C、6.019×109 |
| D、6.019×1010 |
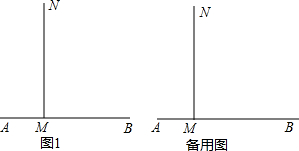 已知:如图1,射线MN⊥AB,点C从M出发,沿射线MN运动,AM=1,MB=4.
已知:如图1,射线MN⊥AB,点C从M出发,沿射线MN运动,AM=1,MB=4. 已知:如图,在△ABC中,CD⊥AB于D,BE⊥AC于E,AD=AE.求证:AB=AC.
已知:如图,在△ABC中,CD⊥AB于D,BE⊥AC于E,AD=AE.求证:AB=AC.