题目内容
2.计算题:(1)$\frac{1-\sqrt{2}}{2}$•$\frac{1+\sqrt{2}}{2}$
(2)(3+$\sqrt{10}$)100(3-$\sqrt{10}$)101
(3)($\sqrt{a}$+$\sqrt{b}$)2-($\sqrt{a}$-$\sqrt{b}$)2
(4)$\frac{2}{3}$$\sqrt{27{a}^{3}}$-a2$\sqrt{\frac{3}{a}}$+6a$\sqrt{\frac{a}{3}}$.
分析 (1)利用平方差公式计算;
(2)先利用积的乘方得到原式=[(3+$\sqrt{10}$)(3-$\sqrt{10}$)]100•(3-$\sqrt{10}$),然后利用平方差公式计算;
(3)先利用完全平方公式展开,然后合并即可;
(4)先把各二次根式化简为最简二次根式,然后合并即可.
解答 解:(1)原式=$\frac{1-(\sqrt{2})^{2}}{4}$=-$\frac{1}{4}$;
(2)原式=[(3+$\sqrt{10}$)(3-$\sqrt{10}$)]100•(3-$\sqrt{10}$)
=(9-10)100•(3-$\sqrt{10}$)
=3-$\sqrt{10}$;
(3)原式=a+2$\sqrt{ab}$+b-(a-2$\sqrt{ab}$+b)
=a+2$\sqrt{ab}$+b-a+2$\sqrt{ab}$-b
=4$\sqrt{ab}$;
(4)原式=2a$\sqrt{3a}$-a$\sqrt{3a}$+2a$\sqrt{3a}$
=3a$\sqrt{3a}$.
点评 本题考查了二次根式的混合运算:先把各二次根式化简为最简二次根式,然后进行二次根式的乘除运算,再合并即可.

练习册系列答案
相关题目
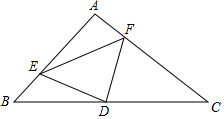 如图所示,在直角△ABC中,∠A=90°,AB=AC,点D为斜边BC上的中点,点E、F分别在直角边AB、AC上,且∠EDF=90°,求证:BE=AF.
如图所示,在直角△ABC中,∠A=90°,AB=AC,点D为斜边BC上的中点,点E、F分别在直角边AB、AC上,且∠EDF=90°,求证:BE=AF. 已知△ABC,利用三角板画平行线.
已知△ABC,利用三角板画平行线.