题目内容
某市一项民生改造工程,由甲、乙两工程队合作20天可完成,若单独完成此项工程,甲工程对所用天数是乙工程队的2倍.
(1)甲、乙两工程队单独完成此项工程各需要多少天?
(2)甲工程队单独做a天后,再由甲、乙两工程队合作 (用含a的代数式表示)可完成此项工程.已知甲工程队施工费每天1万元,乙工程队每天施工费2.5万元,求甲工程队要单独施工多少天后,再由甲、乙两工程队合作完成剩下的工程,才能使工程费不超过64万元.
(1)甲、乙两工程队单独完成此项工程各需要多少天?
(2)甲工程队单独做a天后,再由甲、乙两工程队合作
考点:分式方程的应用,一元一次不等式的应用
专题:
分析:(1)根据题意结合总工作量为1,进而表示出两队每天完成的工作情况,进而得出答案;
(2)首先表示出甲、乙两工程队合作的天数,进而利用两队施工费用得出不等式求出即可.
(2)首先表示出甲、乙两工程队合作的天数,进而利用两队施工费用得出不等式求出即可.
解答:解:(1)设乙工程队单独完成此项工程需要x天,
由题意得:
+
=
,
解得:x=30,
经检验:x=30是原分式方程的解,
2x=60.
答:甲、乙两工程队单独完成此项工程各需要60天,30天;
(2)甲工程队单独做a天后,再由甲、乙两工程队合作:(1-a×
)÷(
+
)=
(天),
由题意可得:1•a+(1+2.5)•
≤64,
解得:a≥36,
答:甲工程队要单独施工36天后,再由甲、乙两工程队合作完成剩下的工程,才能使工程费不超过64万元.
故答案为:
天.
由题意得:
| 1 |
| 2x |
| 1 |
| x |
| 1 |
| 20 |
解得:x=30,
经检验:x=30是原分式方程的解,
2x=60.
答:甲、乙两工程队单独完成此项工程各需要60天,30天;
(2)甲工程队单独做a天后,再由甲、乙两工程队合作:(1-a×
| 1 |
| 60 |
| 1 |
| 30 |
| 1 |
| 60 |
| 60-a |
| 3 |
由题意可得:1•a+(1+2.5)•
| 60-a |
| 3 |
解得:a≥36,
答:甲工程队要单独施工36天后,再由甲、乙两工程队合作完成剩下的工程,才能使工程费不超过64万元.
故答案为:
| 60-a |
| 3 |
点评:此题主要考查了分式方程的应用以及不等式的应用,关键是正确理解题意,找出题目中的等量关系,列出方程.

练习册系列答案
相关题目
在下列方程中,关于x的分式方程的个数有( )
①
=4;②
=4;③
=1;④
=6.
①
| x |
| 5 |
| 6 |
| x |
| x2-9 |
| x+1 |
| 1 |
| x+2 |
| A、2个 | B、3个 | C、4个 | D、1个 |
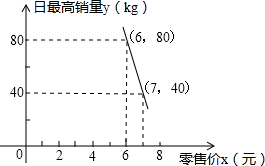 某水果经销商到水果批发市场批发某种水果时了解到如下行情:每千克水果的批发价为4元,经调查,经销商销售该水果的日最高销量与零售价之间的函数关系如图中直线AB所示,该经销商准备购进一定量的水果,且在销售时当日零售价保持不变,考虑到保鲜水果要增加成本,因此经销商要确保每天批发进来的水果全部售完.
某水果经销商到水果批发市场批发某种水果时了解到如下行情:每千克水果的批发价为4元,经调查,经销商销售该水果的日最高销量与零售价之间的函数关系如图中直线AB所示,该经销商准备购进一定量的水果,且在销售时当日零售价保持不变,考虑到保鲜水果要增加成本,因此经销商要确保每天批发进来的水果全部售完.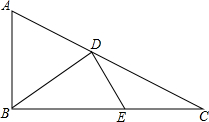 如图,△ABC中,∠ABC=90°,BC=2AB=4,D是AC上一动点,E是BC上一动点,则当BD+DE的值最小时,CE的长为
如图,△ABC中,∠ABC=90°,BC=2AB=4,D是AC上一动点,E是BC上一动点,则当BD+DE的值最小时,CE的长为