题目内容
20.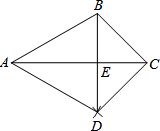 如图,已知△ABC,按如下步骤作图:
如图,已知△ABC,按如下步骤作图:①以A为圆心,AB长为半径画弧;
②以C为圆心,CB长为半径画弧,两弧相交于点D;
③连接BD,与AC交于点E,连接AD,CD.
(1)求证:△ABC≌△ADC;
(2)若∠BAC=30°,∠BCA=45°,AC=4,求BE的长.
分析 (1)利用SSS定理证得结论;
(2)设BE=x,利用特殊角的三角函数易得AE的长,由∠BCA=45°易得CE=BE=x,解得x,得CE的长.
解答 (1)证明:在△ABC与△ADC中,
$\left\{\begin{array}{l}{AB=AD}\\{BC=CD}\\{AC=AC}\end{array}\right.$,
∴△ABC≌△ADC(SSS);
(2)解:设BE=x,
∵∠BAC=30°,
∴∠ABE=60°,
∴AE=tan60°•x=$\sqrt{3}$x,
∵△ABC≌△ADC,
∴CB=CD,∠BCA=∠DCA,
∵∠BCA=45°,
∴∠BCA=∠DCA=45°,
∴∠CBD=∠CDB=45°,
∴CE=BE=x,
∴$\sqrt{3}$x+x=4,
∴x=2$\sqrt{3}$-2,
∴BE=2$\sqrt{3}$-2.
点评 本题主要考查了全等三角形的判定及性质,特殊角的三角函数,利用方程思想,综合运用全等三角形的性质和判定定理是解答此题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
10. 如图,矩形ABCD中,AB=8,BC=4.点E在边AB上,点F在边CD上,点G、H在对角线AC上.若四边形EGFH是菱形,则AE的长是( )
如图,矩形ABCD中,AB=8,BC=4.点E在边AB上,点F在边CD上,点G、H在对角线AC上.若四边形EGFH是菱形,则AE的长是( )
 如图,矩形ABCD中,AB=8,BC=4.点E在边AB上,点F在边CD上,点G、H在对角线AC上.若四边形EGFH是菱形,则AE的长是( )
如图,矩形ABCD中,AB=8,BC=4.点E在边AB上,点F在边CD上,点G、H在对角线AC上.若四边形EGFH是菱形,则AE的长是( )| A. | 2$\sqrt{5}$ | B. | 3$\sqrt{5}$ | C. | 5 | D. | 6 |
15.若二次函数y=x2+bx的图象的对称轴是经过点(2,0)且平行于y轴的直线,则关于x的方程x2+bx=5的解为( )
| A. | x1=0,x2=4 | B. | x1=1,x2=5 | C. | x1=1,x2=-5 | D. | x1=-1,x2=5 |
5. 将正方形ABCD绕点A按逆时针方向旋转30°,得正方形AB1C1D1,B1C1交CD于点E,AB=$\sqrt{3}$,则四边形AB1ED的内切圆半径为( )
将正方形ABCD绕点A按逆时针方向旋转30°,得正方形AB1C1D1,B1C1交CD于点E,AB=$\sqrt{3}$,则四边形AB1ED的内切圆半径为( )
 将正方形ABCD绕点A按逆时针方向旋转30°,得正方形AB1C1D1,B1C1交CD于点E,AB=$\sqrt{3}$,则四边形AB1ED的内切圆半径为( )
将正方形ABCD绕点A按逆时针方向旋转30°,得正方形AB1C1D1,B1C1交CD于点E,AB=$\sqrt{3}$,则四边形AB1ED的内切圆半径为( )| A. | $\frac{\sqrt{3}+1}{2}$ | B. | $\frac{3-\sqrt{3}}{2}$ | C. | $\frac{\sqrt{3}+1}{3}$ | D. | $\frac{3-\sqrt{3}}{3}$ |
12.下列命题是真命题的是( )
| A. | 对角线互相平分的四边形是平行四边形 | |
| B. | 对角线相等的四边形是矩形 | |
| C. | 对角线互相垂直的四边形是菱形 | |
| D. | 对角线互相垂直的四边形是正方形 |
9.数5的算术平方根为( )
| A. | $\sqrt{5}$ | B. | 25 | C. | ±25 | D. | ±$\sqrt{5}$ |
10.下列所述图形中,既是中心对称图形,又是轴对称图形的是( )
| A. | 矩形 | B. | 平行四边形 | C. | 正五边形 | D. | 正三角形 |

