题目内容
5. 将正方形ABCD绕点A按逆时针方向旋转30°,得正方形AB1C1D1,B1C1交CD于点E,AB=$\sqrt{3}$,则四边形AB1ED的内切圆半径为( )
将正方形ABCD绕点A按逆时针方向旋转30°,得正方形AB1C1D1,B1C1交CD于点E,AB=$\sqrt{3}$,则四边形AB1ED的内切圆半径为( )| A. | $\frac{\sqrt{3}+1}{2}$ | B. | $\frac{3-\sqrt{3}}{2}$ | C. | $\frac{\sqrt{3}+1}{3}$ | D. | $\frac{3-\sqrt{3}}{3}$ |
分析 作∠DAF与∠AB1G的角平分线交于点O,则O即为该圆的圆心,过O作OF⊥AB1,AB=$\sqrt{3}$,再根据直角三角形的性质便可求出OF的长,即该四边形内切圆的圆心.
解答  解:作∠DAF与∠AB1G的角平分线交于点O,过O作OF⊥AB1,
解:作∠DAF与∠AB1G的角平分线交于点O,过O作OF⊥AB1,
则∠OAF=30°,∠AB1O=45°,
故B1F=OF=$\frac{1}{2}$OA,
设B1F=x,则AF=$\sqrt{3}$-x,
故($\sqrt{3}$-x)2+x2=(2x)2,
解得x=$\frac{-\sqrt{3}+3}{2}$或x=$\frac{-\sqrt{3}-3}{2}$(舍去),
∴四边形AB1ED的内切圆半径为:$\frac{-\sqrt{3}+3}{2}$.
故选:B.
点评 本题考查了旋转的性质三角形的内切圆,正方形的性质,要熟练掌握正方形的性质及直角三角形的性质,是解答此题的关键.

练习册系列答案
相关题目
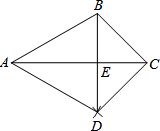
15. 如图,菱形ABCD中,对角线AC、BD相交于点O,H为AD边的中点,若菱形ABCD的周长为20,则OH的长为( )
如图,菱形ABCD中,对角线AC、BD相交于点O,H为AD边的中点,若菱形ABCD的周长为20,则OH的长为( )
 如图,菱形ABCD中,对角线AC、BD相交于点O,H为AD边的中点,若菱形ABCD的周长为20,则OH的长为( )
如图,菱形ABCD中,对角线AC、BD相交于点O,H为AD边的中点,若菱形ABCD的周长为20,则OH的长为( )| A. | 2 | B. | 2.5 | C. | 3 | D. | 3.5 |
16.电视剧《铁血将军》在我市拍摄,该剧展示了抗日英雄范筑先的光辉形象.某校为了了解学生对“民族英雄范筑先”的知晓情况,从全校2400名学生中随机抽取了100名学生进行调查.在这次调查中,样本是( )
| A. | 2400名学生 | |
| B. | 100名学生 | |
| C. | 所抽取的100名学生对“民族英雄范筑先”的知晓情况 | |
| D. | 每一名学生对“民族英雄范筑先”的知晓情况 |
13.已知抛物线y=-$\frac{1}{6}$x2+$\frac{3}{2}$x+6与x轴交于点A,点B,与y轴交于点C.若D为AB的中点,则CD的长为( )
| A. | $\frac{15}{4}$ | B. | $\frac{9}{2}$ | C. | $\frac{13}{2}$ | D. | $\frac{15}{2}$ |
17.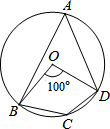 如图,四边形ABCD为⊙O的内接四边形,已知∠BOD=100°,则∠BCD的度数为( )
如图,四边形ABCD为⊙O的内接四边形,已知∠BOD=100°,则∠BCD的度数为( )
 如图,四边形ABCD为⊙O的内接四边形,已知∠BOD=100°,则∠BCD的度数为( )
如图,四边形ABCD为⊙O的内接四边形,已知∠BOD=100°,则∠BCD的度数为( )| A. | 50° | B. | 80° | C. | 100° | D. | 130° |
14.在△ABC中,∠A:∠B:∠C=3:4:5,则∠C等于( )
| A. | 45° | B. | 60° | C. | 75° | D. | 90° |
 如图,已知△ABC,按如下步骤作图:
如图,已知△ABC,按如下步骤作图:


