题目内容
18.一数列a1,a2,a3,…an,a1=-1,a2=$\frac{1}{1-{a}_{1}}$,a3=$\frac{1}{1-{a}_{2}}$,…an$\frac{1}{1-{a}_{n-1}}$=,求出a1+a2+a3+…+a2015的值.分析 首先求得a2,a3,a4,a5,…找出数字循环的规律,利用规律分组求和得出答案即可.
解答 解:∵a1=-1,
∴a2=$\frac{1}{1-{a}_{1}}$=$\frac{1}{2}$,
a3=$\frac{1}{1-{a}_{2}}$=2,
a4=$\frac{1}{1-{a}_{3}}$=-1,
…
∴-1,$\frac{1}{2}$,2三个数字依次不断循环出现,
∵2015÷3=671…2,
∴a1+a2+a3+…+a2015=671×(-1+$\frac{1}{2}$+2)-1+$\frac{1}{2}$=1006.
点评 此题考查数字的变化规律,找出数字之间的运算规律,利用循环的规律解决问题.

练习册系列答案
 千里马走向假期期末仿真试卷寒假系列答案
千里马走向假期期末仿真试卷寒假系列答案
相关题目
10.已知2是方程x2-ax+2=0的一个根,则方程的另一个根为( )
| A. | -1 | B. | 1 | C. | 2 | D. | 3 |
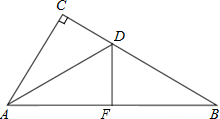 如图,在△ABC中,∠ACB=90°,AD是∠CAB的平分线,△ACD沿AD翻折,C点落在边AB上的点F处.己知AC=6,BC=8,求DF的长.
如图,在△ABC中,∠ACB=90°,AD是∠CAB的平分线,△ACD沿AD翻折,C点落在边AB上的点F处.己知AC=6,BC=8,求DF的长. 如图,BP是∠ABC的平分线,DP是∠CDA的平分线,BP与DP交于P,若∠A=40°,∠C=76°,求∠P的大小.
如图,BP是∠ABC的平分线,DP是∠CDA的平分线,BP与DP交于P,若∠A=40°,∠C=76°,求∠P的大小.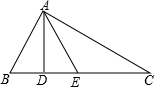 如图,在△ABC中,∠BAC=90°,AD⊥BC,∠BAD=30°,AE为BC边上的中线,求证:AE=AB.
如图,在△ABC中,∠BAC=90°,AD⊥BC,∠BAD=30°,AE为BC边上的中线,求证:AE=AB. 已知:如图,在△ABC中,AC=2.BC=3.∠C=60°. 求△ABC外接圆⊙O的半径r.
已知:如图,在△ABC中,AC=2.BC=3.∠C=60°. 求△ABC外接圆⊙O的半径r.