Question

如图，直线y=

3

x，点A₁坐标为（1，0），过点A₁作x的垂线交直线于点B₁，以原点O为圆心，OB₁长为半径画弧交x轴于点A₂；再过点A₂x的垂线交直线于点B₂，以原点O为圆心，OB₂长为半径画弧交x轴于点A₃，…，按此作法进行下去，点A₃的坐标为（

 

，

 

）．

Answer 1

考点：一次函数图象上点的坐标特征

专题：规律型

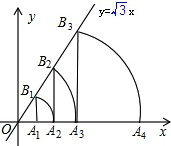
分析：根据点A₁坐标为（1，0），且B₁A₁⊥x轴，可得出B₁的横坐标为1，将其横坐标代入直线解析式就可以求出B₁的坐标，就可以求出A₁B₁的值，OA₁的值，根据锐角三角函数值就可以求出∠xOB₃的度数，从而求出OB₁的值，就可以求出OA₂值，同理可以求出OB₂、OB₃…，从而寻找出点A₂、A₃…的坐标规律，最后求出A₃的坐标．

解答：解：∵点A₁坐标为（1，0），
∴OA₁=1．
∵B₁A₁⊥x轴，
∴点B₁的横坐标为1，且点B₁在直线上，
∴y=

3

，
∴B₁（1，

3

），
∴A₁B₁=

3

．
在Rt△A₁B₁O中由勾股定理，得OB₁=2，
∴sin∠OB₁A₁=

1

2

，
∴∠OB₁A₁=30°，
∴∠OB₁A₁=∠OB₂A₂=∠OB₃A₃=…=∠OB_nA_n=30°．
∵OA₂=OB₁=2，
∴A₂（2，0）．
在Rt△OB₂A₂中，
∵OB₂=2OA₂=4
∴OA₃=4，
∴A₃（4，0）．
故答案为：（4，0）．

点评：本题考查的是一次函数图象上点的坐标特点，涉及到直角三角形的性质，特别是30°所对的直角边等于斜边的一半的运用，点的坐标与函数图象的关系等知识．