题目内容
 如图,DB为半圆的直径,且 BD=2,A为BD延长线上一点,AC切半圆于点E,BC⊥AC于点C,交半圆于点F.
如图,DB为半圆的直径,且 BD=2,A为BD延长线上一点,AC切半圆于点E,BC⊥AC于点C,交半圆于点F.(1)连接BE,求证:BE平分∠DBC;
(2)当AD为何值时,四边形BOEF为菱形?
考点:切线的性质,菱形的判定
专题:证明题
分析:(1)证明:连结OE,如图,根据切线的性质得OE⊥AC,而BC⊥AC,则OE∥BC,根据平行线的性质得∠2=∠3,加上∠1=∠3,所以∠1=∠2;
(2)连结OF,由于OE∥BF,则当EF∥OB时,四边形BOEF为平行四边形,加上OB=OE,则此时四边形BOEF为菱形,所以EF=BF=OB=OE=2,可判定△OEF和△OBF都是等边三角形,得到∠BOF=∠EOF=60°,于是计算出∠AOE=60°,在Rt△AOE中利用含30度的直角三角形三边的关系可计算出OA=2OE=4,易得AD=OA-OD=2.
(2)连结OF,由于OE∥BF,则当EF∥OB时,四边形BOEF为平行四边形,加上OB=OE,则此时四边形BOEF为菱形,所以EF=BF=OB=OE=2,可判定△OEF和△OBF都是等边三角形,得到∠BOF=∠EOF=60°,于是计算出∠AOE=60°,在Rt△AOE中利用含30度的直角三角形三边的关系可计算出OA=2OE=4,易得AD=OA-OD=2.
解答:(1)证明:连结OE,如图,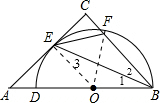
∵AC切半圆于点E,
∴OE⊥AC,
∵BC⊥AC,
∴OE∥BC,
∴∠2=∠3,
而OE=OB,
∴∠1=∠3,
∴∠1=∠2,
∴BE平分∠DBC;
(2)解:连结OF,
∵OE∥BF,
∴当EF∥OB时,四边形BOEF为平行四边形,
而OB=OE,则此时四边形BOEF为菱形,
∴EF=BF=OB=OE=2,
∴△OEF和△OBF都是等边三角形,
∴∠BOF=∠EOF=60°,
∴∠AOE=60°,
在Rt△AOE中,∠A=30°,
∴OA=2OE=4,
∴AD=OA-OD=4-2=2,
即当AD为2时,四边形BOEF为菱形.

∵AC切半圆于点E,
∴OE⊥AC,
∵BC⊥AC,
∴OE∥BC,
∴∠2=∠3,
而OE=OB,
∴∠1=∠3,
∴∠1=∠2,
∴BE平分∠DBC;
(2)解:连结OF,
∵OE∥BF,
∴当EF∥OB时,四边形BOEF为平行四边形,
而OB=OE,则此时四边形BOEF为菱形,
∴EF=BF=OB=OE=2,
∴△OEF和△OBF都是等边三角形,
∴∠BOF=∠EOF=60°,
∴∠AOE=60°,
在Rt△AOE中,∠A=30°,
∴OA=2OE=4,
∴AD=OA-OD=4-2=2,
即当AD为2时,四边形BOEF为菱形.
点评:本题考查了切线的性质:圆的切线垂直于经过切点的半径.运用切线的性质来进行计算或论证,常通过作辅助线连接圆心和切点,利用垂直构造直角三角形解决有关问题.也考查了菱形的判定.

练习册系列答案
相关题目
下列说法正确的是( )
| A、做抛掷硬币的实验,如果没有硬币用图钉代替硬币,做出的实验结果是一致的 |
| B、抛掷一枚质地均匀的硬币,已连续掷出5次正面,则第6次一定掷出背面 |
| C、某种彩票中奖的概率是1%,因此买100张该彩票一定会中奖 |
| D、天气预报说明天下雨的概率是50%,也就是说明天下雨和不下雨的机会是均等的 |
下列事件中属于随机事件的是( )
| A、通常加热到100℃时,水沸腾 |
| B、某射击运动员射击一次,命中靶心 |
| C、若a是实数,则|a|≥0 |
| D、在一个仅装着白球和黑球的袋中摸球,摸出红球 |
 如图,在菱形ABCD中,E、F分别是AC、BC的中点,如果EF=5,那么菱形ABCD的周长
如图,在菱形ABCD中,E、F分别是AC、BC的中点,如果EF=5,那么菱形ABCD的周长 如图,反比例函数y=
如图,反比例函数y=



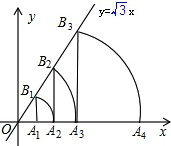 如图,直线y=
如图,直线y=