题目内容
在△ABC中,∠A、∠B为锐角,且|tanA-1|+(
-cosB)2=0,则∠C= °.
| 1 |
| 2 |
考点:特殊角的三角函数值,非负数的性质:绝对值,非负数的性质:偶次方
专题:
分析:根据非负数的性质求出tanA和cosB的值,然后求出∠A、∠B的度数,最后求出∠C.
解答:解:由题意得,tanA=1,cosB=
,
则∠A=45°,∠B=60°,
则∠C=180°-45°-60°=75°.
故答案为:75.
| 1 |
| 2 |
则∠A=45°,∠B=60°,
则∠C=180°-45°-60°=75°.
故答案为:75.
点评:本题考查了特殊角的三角函数值,解答本题的关键是掌握几个特殊角的三角函数值.

练习册系列答案
 天天向上口算本系列答案
天天向上口算本系列答案
相关题目
下列四种汽车标志中,不是轴对称图形的是( )
A、 |
B、 |
C、 |
D、 |
下列四组数据中,不能作为直角三角形的三边长的是( )
| A、7,24,25 |
| B、6,8,10 |
| C、9,12,17 |
| D、3,4,5 |
 如图,反比例函数y=
如图,反比例函数y=
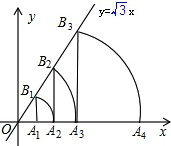 如图,直线y=
如图,直线y=