题目内容
16.已知关于x的方程x2-(k+1)x+$\frac{1}{4}{k}^{2}$+1=0有两个实数根.(1)求k得取值范围;
(2)若方程的两实数根分别为x1、x2,且满足|x1|+|x2|=4x1x2-5,求k的值.
分析 (1)根据方程有两个实数根可得△=(k-1)2-4($\frac{1}{4}$k2+1)≥0,解不等式可得k的范围;
(2)由韦达定理可得x1+x2=k+1>0、x1•x2=$\frac{1}{4}$k2+1>0,根据|x1|+|x2|=4x1x2-5可得k+1=4($\frac{1}{4}$k2+1)-5,解方程结合k的取值范围可得k的值.
解答 解:(1)∵原方程有两个实数根,
∴△=(k-1)2-4($\frac{1}{4}$k2+1)=2k-3≥0
解得:k≥$\frac{3}{2}$;
(2)∵k≥$\frac{3}{2}$,
∴x1+x2=k+1>0.
又∵x1•x2=$\frac{1}{4}$k2+1>0,
∴x1>0,x2>0,
∴|x1|+|x2|=x1+x2=k+1.
∵|x1|+|x2|=4x1x2-5,
∴k+1=4($\frac{1}{4}$k2+1)-5,
∴k2-k-2=0,
∴k1=-1,k2=2,
又∵k≥$\frac{3}{2}$,
∴k=2.
点评 本题考查了一元二次方程ax2+bx+c=0(a≠0,a,b,c为常数)的根的判别式△=b2-4ac及韦达定理的应用.当△>0时,方程有两个不相等的实数根;当△=0时,方程有两个相等的实数根;当△<0时,方程没有实数根.

练习册系列答案
相关题目
6. 寒假结束了,开学后小明对本校七年级部分同学寒假阅读总时间(结果保留整10小时)进行了抽样调查,所得数据整理后制作成如图所示的频数分布直方图.观察这个频数分布直方图,给出如下结论,正确的是( )
寒假结束了,开学后小明对本校七年级部分同学寒假阅读总时间(结果保留整10小时)进行了抽样调查,所得数据整理后制作成如图所示的频数分布直方图.观察这个频数分布直方图,给出如下结论,正确的是( )
 寒假结束了,开学后小明对本校七年级部分同学寒假阅读总时间(结果保留整10小时)进行了抽样调查,所得数据整理后制作成如图所示的频数分布直方图.观察这个频数分布直方图,给出如下结论,正确的是( )
寒假结束了,开学后小明对本校七年级部分同学寒假阅读总时间(结果保留整10小时)进行了抽样调查,所得数据整理后制作成如图所示的频数分布直方图.观察这个频数分布直方图,给出如下结论,正确的是( )| A. | 小明调查了100名同学 | |
| B. | 所得数据的众数是40小时 | |
| C. | 所得数据的中位数是30小时 | |
| D. | 全区有七年级学生6000名,寒假阅读总时间在20小时(含20小时)以上的约有5000名 |
4.一只不透明的袋子中装有3个黑球和2个白球,这些除颜色外无其他差别,从中任意摸出3个球,下列事件是必然事件的为( )
| A. | 至少有1个球是黑球 | B. | 至少有1个球是白球 | ||
| C. | 至少有2个球是黑球 | D. | 至少有2个球是白球 |
11.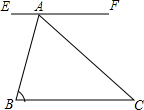 如图,EF∥BC,AC平分∠BAF,∠B=70°,则∠C的度数是( )
如图,EF∥BC,AC平分∠BAF,∠B=70°,则∠C的度数是( )
 如图,EF∥BC,AC平分∠BAF,∠B=70°,则∠C的度数是( )
如图,EF∥BC,AC平分∠BAF,∠B=70°,则∠C的度数是( )| A. | 70° | B. | 60° | C. | 55° | D. | 50° |
1.假如要给地球缝制一件外衣,那么所需的布料应不少于( )
| A. | 5.1亿km2 | B. | 5.1亿km | C. | 5.1亿km3 | D. | 5.11km3 |