题目内容
11.先化简再求值:($\frac{x}{x+1}$-1)÷$\frac{1}{{x}^{2}-1}$,其中x=2016.分析 先把括号内通分,再把除法运算化为乘法运算,然后约分得到原式=-x+1,再把x的值代入计算即可.
解答 解:原式=$\frac{x-(x+1)}{x+1}$•(x+1)(x-1)
=-x+1,
当x=2016时,原式=-2016+1=-2015.
点评 本题考查了分式的化简求值:先把分式化简后,再把分式中未知数对应的值代入求出分式的值.在化简的过程中要注意运算顺序和分式的化简.化简的最后结果分子、分母要进行约分,注意运算的结果要化成最简分式或整式.

练习册系列答案
 文敬图书课时先锋系列答案
文敬图书课时先锋系列答案
相关题目
2.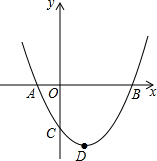 如图,二次函数y=ax2+bx+c(a>0)图象的顶点为D,其图象与x轴的交点A、B的横坐标分别为-1和3,则下列结论正确的是( )
如图,二次函数y=ax2+bx+c(a>0)图象的顶点为D,其图象与x轴的交点A、B的横坐标分别为-1和3,则下列结论正确的是( )
 如图,二次函数y=ax2+bx+c(a>0)图象的顶点为D,其图象与x轴的交点A、B的横坐标分别为-1和3,则下列结论正确的是( )
如图,二次函数y=ax2+bx+c(a>0)图象的顶点为D,其图象与x轴的交点A、B的横坐标分别为-1和3,则下列结论正确的是( )| A. | 2a-b=0 | B. | a+b+c>0 | ||
| C. | 3a-c=0 | D. | 当a=$\frac{1}{2}$时,△ABD是等腰直角三角形 |
19.下列运算正确的是( )
| A. | (-$\frac{3}{2}$)2=-$\frac{9}{4}$ | B. | (3a2)3=9a6 | C. | 5-3÷5-5=$\frac{1}{25}$ | D. | $\sqrt{8}-\sqrt{50}=-3\sqrt{2}$ |
16.已知一次函数y=kx+b-x的图象与x轴的正半轴相交,且函数值y随自变量x的增大而增大,则k,b的取值情况为( )
| A. | k>1,b<0 | B. | k>1,b>0 | C. | k>0,b>0 | D. | k>0,b<0 |
 一次函数y=ax+b和反比例函数y=$\frac{c}{x}$在同一平面直角坐标系中的图象如图所示,则二次函数y=ax2+bx+c的图象大致为( )
一次函数y=ax+b和反比例函数y=$\frac{c}{x}$在同一平面直角坐标系中的图象如图所示,则二次函数y=ax2+bx+c的图象大致为( )

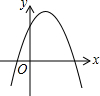


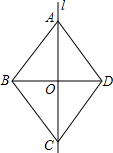 如图,四边形ABCD是轴对称图形,且直线AC是对称轴,AB∥CD,则下列结论:①AC⊥BD;②AD∥BC;③四边形ABCD是菱形;④△ABD≌△CDB.其中正确的是①②③④(只填写序号)
如图,四边形ABCD是轴对称图形,且直线AC是对称轴,AB∥CD,则下列结论:①AC⊥BD;②AD∥BC;③四边形ABCD是菱形;④△ABD≌△CDB.其中正确的是①②③④(只填写序号)