题目内容
1.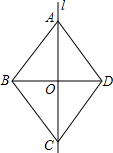 如图,四边形ABCD是轴对称图形,且直线AC是对称轴,AB∥CD,则下列结论:①AC⊥BD;②AD∥BC;③四边形ABCD是菱形;④△ABD≌△CDB.其中正确的是①②③④(只填写序号)
如图,四边形ABCD是轴对称图形,且直线AC是对称轴,AB∥CD,则下列结论:①AC⊥BD;②AD∥BC;③四边形ABCD是菱形;④△ABD≌△CDB.其中正确的是①②③④(只填写序号)
分析 根据轴对称图形的性质,结合菱形的判定方法以及全等三角形的判定方法分析得出答案.
解答  解:因为l是四边形ABCD的对称轴,AB∥CD,
解:因为l是四边形ABCD的对称轴,AB∥CD,
则AD=AB,∠1=∠2,∠1=∠4,
则∠2=∠4,
∴AD=DC,
同理可得:AB=AD=BC=DC,
所以四边形ABCD是菱形.
根据菱形的性质,可以得出以下结论:
所以①AC⊥BD,正确;
②AD∥BC,正确;
③四边形ABCD是菱形,正确;
④在△ABD和△CDB中
∵$\left\{\begin{array}{l}{AB=BC}\\{AD=DC}\\{BD=BD}\end{array}\right.$
∴△ABD≌△CDB(SSS),正确.
故答案为:①②③④.
点评 此题考查了轴对称以及菱形的判断与菱形的性质,注意:对称轴垂直平分对应点的连线,对应角相等,对应边相等.

练习册系列答案
 周周清检测系列答案
周周清检测系列答案 轻巧夺冠周测月考直通高考系列答案
轻巧夺冠周测月考直通高考系列答案
相关题目
12.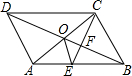 如图,?ABCD的对角线AC,BD交于点O,CE平分∠BCD交AB于点E,交BD于点F,且∠ABC=60°,AB=2BC,连接OE.下列结论:
如图,?ABCD的对角线AC,BD交于点O,CE平分∠BCD交AB于点E,交BD于点F,且∠ABC=60°,AB=2BC,连接OE.下列结论:
①∠ACD=30°;②S?ABCD=AC•BC;③OE:AC=$\sqrt{3}$:6;④S△OCF=2S△OEF
成立的个数有( )
 如图,?ABCD的对角线AC,BD交于点O,CE平分∠BCD交AB于点E,交BD于点F,且∠ABC=60°,AB=2BC,连接OE.下列结论:
如图,?ABCD的对角线AC,BD交于点O,CE平分∠BCD交AB于点E,交BD于点F,且∠ABC=60°,AB=2BC,连接OE.下列结论:①∠ACD=30°;②S?ABCD=AC•BC;③OE:AC=$\sqrt{3}$:6;④S△OCF=2S△OEF
成立的个数有( )
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
9. 如图,在△ABC中,D、E分别为AB、AC边上的点,DE∥BC,BE与CD相交于点F,则下列结论一定正确的是( )
如图,在△ABC中,D、E分别为AB、AC边上的点,DE∥BC,BE与CD相交于点F,则下列结论一定正确的是( )
 如图,在△ABC中,D、E分别为AB、AC边上的点,DE∥BC,BE与CD相交于点F,则下列结论一定正确的是( )
如图,在△ABC中,D、E分别为AB、AC边上的点,DE∥BC,BE与CD相交于点F,则下列结论一定正确的是( )| A. | $\frac{AD}{AB}$=$\frac{AE}{AC}$ | B. | $\frac{DF}{FC}=\frac{AE}{EC}$ | C. | $\frac{AD}{DB}=\frac{DE}{BC}$ | D. | $\frac{DF}{BF}=\frac{EF}{FC}$ |
16.在平面直角坐标系中,将△AOB绕原点O顺时针旋转180°后得到△A1OB1,若点B的坐标为(2,1),则点B的对应点B1的坐标为( )
| A. | (1,2) | B. | (2,-1) | C. | (-2,1) | D. | (-2,-1) |
6.下列图形中,是轴对称图形的是( )
| A. |  | B. |  | C. |  | D. |  |
10.设点A(a,b)是正比例函数y=-$\frac{3}{2}$x图象上的任意一点,则下列等式一定成立的是( )
| A. | 2a+3b=0 | B. | 2a-3b=0 | C. | 3a-2b=0 | D. | 3a+2b=0 |
11. 如图,将△ABC沿着过AB中点D的直线折叠,使点A落在BC边上的A1处,折痕与AC边交于点E,分别过点D、E作BC的垂线,垂足为Q、P,称为第1次操作,记四边形DEPQ的面积为S1;还原纸片后,再将△ADE沿着过AD中点D1的直线折叠,使点A落在DE边上的A2处,折痕与AC边交于点E1,分别过点D1、E1作BC的垂线,垂足为Q1、P1,称为第2次操作,记四边形D1E1P1Q1的面积为S2;按上述方法不断操作下去…,若△ABC的面积为1,则Sn的值为( )
如图,将△ABC沿着过AB中点D的直线折叠,使点A落在BC边上的A1处,折痕与AC边交于点E,分别过点D、E作BC的垂线,垂足为Q、P,称为第1次操作,记四边形DEPQ的面积为S1;还原纸片后,再将△ADE沿着过AD中点D1的直线折叠,使点A落在DE边上的A2处,折痕与AC边交于点E1,分别过点D1、E1作BC的垂线,垂足为Q1、P1,称为第2次操作,记四边形D1E1P1Q1的面积为S2;按上述方法不断操作下去…,若△ABC的面积为1,则Sn的值为( )
 如图,将△ABC沿着过AB中点D的直线折叠,使点A落在BC边上的A1处,折痕与AC边交于点E,分别过点D、E作BC的垂线,垂足为Q、P,称为第1次操作,记四边形DEPQ的面积为S1;还原纸片后,再将△ADE沿着过AD中点D1的直线折叠,使点A落在DE边上的A2处,折痕与AC边交于点E1,分别过点D1、E1作BC的垂线,垂足为Q1、P1,称为第2次操作,记四边形D1E1P1Q1的面积为S2;按上述方法不断操作下去…,若△ABC的面积为1,则Sn的值为( )
如图,将△ABC沿着过AB中点D的直线折叠,使点A落在BC边上的A1处,折痕与AC边交于点E,分别过点D、E作BC的垂线,垂足为Q、P,称为第1次操作,记四边形DEPQ的面积为S1;还原纸片后,再将△ADE沿着过AD中点D1的直线折叠,使点A落在DE边上的A2处,折痕与AC边交于点E1,分别过点D1、E1作BC的垂线,垂足为Q1、P1,称为第2次操作,记四边形D1E1P1Q1的面积为S2;按上述方法不断操作下去…,若△ABC的面积为1,则Sn的值为( )| A. | $\frac{{2}^{2n}-2}{{2}^{2n}}$ | B. | $\frac{{2}^{n}-1}{{2}^{2n-1}}$ | C. | $\frac{{3}^{n}-1}{{2}^{2n}}$ | D. | $\frac{{2}^{n-1}-1}{{2}^{2n}}$ |