题目内容
6.当a,b,c是实数时.求证:方程x2-(a+b)x+(ab-c2)=0必有两个实数根.并求两根相等的条件.分析 先计算判别式的值,得到△=(a+b)2-4(ab-c2),利用完全平方公式得到△=(a-b)2+4c2,则根据非负数的性质可判断△≥0,于是根据判别式的意义可判断方程必有两个实数根;根据判别式的意义,当△=0时,方程有两个相等的实数解,则利用非负数的性质易得a-b=0,c=0.
解答 证明:△=(a+b)2-4(ab-c2)
=(a-b)2+4c2,
∵(a-b)2≥0,4c2≥0,
∴△≥0,
∴方程x2-(a+b)x+(ab-c2)=0必有两个实数根,
当△=0时,方程有两个相等的实数解,此时a-b=0,c=0,即a=b,c=0.
点评 本题考查了根的判别式:一元二次方程ax2+bx+c=0(a≠0)的根与△=b2-4ac有如下关系:当△>0时,方程有两个不相等的两个实数根;当△=0时,方程有两个相等的两个实数根;当△<0时,方程无实数根.

练习册系列答案
 冲刺100分1号卷系列答案
冲刺100分1号卷系列答案
相关题目
5.已知xy>0,将$\sqrt{-\frac{y}{{x}^{2}}}$化为最简二次根式为( )
| A. | $\frac{\sqrt{y}}{x}$ | B. | $\frac{\sqrt{-y}}{x}$ | C. | $\frac{-\sqrt{y}}{x}$ | D. | $\frac{-\sqrt{-y}}{x}$ |
 分别画出这个平房从正面,左面和上面看到的形状图.
分别画出这个平房从正面,左面和上面看到的形状图.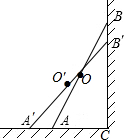 如图,梯子AB靠在墙上,记墙根为C,且∠CBA=20°,现将梯子A向外移到A′,同时梯子的顶端B下移至B′,且∠CB′A′=30°.若梯子AB的长度为6m,求梯子AB的中点O划过的路程.
如图,梯子AB靠在墙上,记墙根为C,且∠CBA=20°,现将梯子A向外移到A′,同时梯子的顶端B下移至B′,且∠CB′A′=30°.若梯子AB的长度为6m,求梯子AB的中点O划过的路程.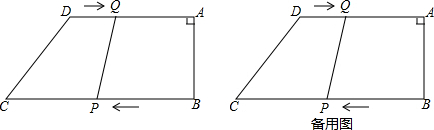
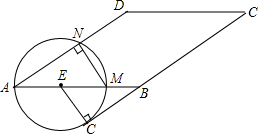 如图,在?ABCD(AB>AD)中,点E在边AB上,以点E为圆心,AE长为半径的⊙E分别交AB、AD于点N、N,与BC所在的直线相切于点G
如图,在?ABCD(AB>AD)中,点E在边AB上,以点E为圆心,AE长为半径的⊙E分别交AB、AD于点N、N,与BC所在的直线相切于点G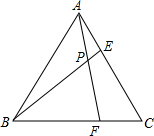 等边三角形ABC的边长为6,在AC,BC边上各取一点E,F,连接AF,BE相交于点P;
等边三角形ABC的边长为6,在AC,BC边上各取一点E,F,连接AF,BE相交于点P;