题目内容
7.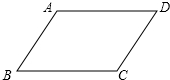 如图,已知?ABCD.
如图,已知?ABCD.(1)作∠B的平分线交AD于点E;(用尺规作图法,保留作图痕迹,不要求写作法)
(2)若□ABCD的周长为20,CD=4,求DE的长.
分析 (1)以点B为圆心,任意长为半径画弧,交AB,BC于两点,分别以这两点为圆心,大于这两点的距离为半径画弧,在△ABC内交于一点O,作射线BO,交AD于点E即可;
(2)利用角平分线的性质以及平行线的性质求出∠ABE=∠AEB,得出AE=AB=4,再由平行四边形的周长求出AD,即可得出结果.
解答 解:(1)如图所示:
(2)∵BE平分∠ABC,
∴∠ABE=∠EBC,
∵四边形ABCD是平行四边形,
∴AD∥BC,AB=CD=4,AD=BC,
∴∠AEB=∠EBC,
∴∠ABE=∠AEB,
∴AE=AB=4,
∵?ABCD的周长为20,
∴AB+AD=10,
∴AD=6,
∴DE=AD-AE=6-4=2.
点评 本题考查了三角形的角平分线的画法以及角平分线的性质以及平行线的性质等知识,利用角平分线的性质得出AE=AB是解题关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
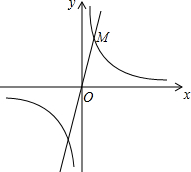 如图,在平面直角坐标系xOy中,反比例函数y=$\frac{4}{x}$的图象与正比例函数y=kx的图象的一个交点为M(1,b).
如图,在平面直角坐标系xOy中,反比例函数y=$\frac{4}{x}$的图象与正比例函数y=kx的图象的一个交点为M(1,b). 如图,AB∥CD,∠BAC与∠ACD的平分线交于点H,求证:△AHC是直角三角形.
如图,AB∥CD,∠BAC与∠ACD的平分线交于点H,求证:△AHC是直角三角形.