题目内容
19. 画图,填空并说明理由
画图,填空并说明理由(1)画出图中△ABC的中线AD;
(2)在图中分别画出△ABD的高BE,△ACD的高CF;
(3)猜想,BE,CF的关系是相等.理由:全等三角形,对应边相等.
分析 (1)首先找出BC中点,再连接AD即可;
(2)利用直角三角板,一条直角边与BD重合,沿BC平移使另一直角边过B,再作垂线即可,同法可得△ACD的高CF;
(3)证明△BED≌△CFD可得BE=CF即可.
解答 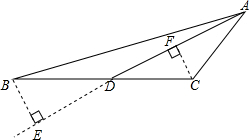 解:(1)如图所示:
解:(1)如图所示:
(2)如图所示:
(3)BE=CF,
理由:∵DA是中线,
∴BD=CD,
∵CF⊥AD,BE⊥AD,
∴∠CFD=∠BED,
在△BED和△CFD中,
$\left\{\begin{array}{l}{∠CFD=∠BED}\\{∠BDE=∠CDF}\\{BD=CD}\end{array}\right.$,
∴△BED≌△CFD(AAS),
∴BE=CF(全等三角形对应边相等).
故答案为:相等;全等三角形对应边相等.
点评 此题主要考查了复杂作图以及全等三角形的判定和性质,关键是掌握中线和高线的定义以及作法.

练习册系列答案
相关题目
 如图:DF⊥AB于F,∠A=40°,∠B=48°,则∠ACB=92°,∠AED=130°.
如图:DF⊥AB于F,∠A=40°,∠B=48°,则∠ACB=92°,∠AED=130°.