题目内容
已知在△ABC中,AB=
,AC=2
,BC=3.
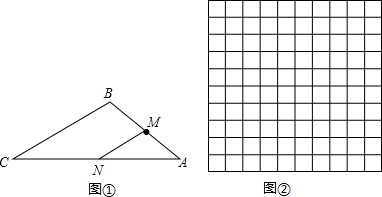
(1)如图①,点M为AB的中点,在线段AC上取点N,使△AMN与△ABC相似,求线段MN的长;
(2)如图,是由100个边长为1的小正方形组成的10×10的正方形网格,设顶点在这些小正方形顶点的三角形为格点三角形.
①请你在所给的网格中画出格点△A1B1C1与△ABC全等(画出一个即可,不需证明);
②试直接写出所给的网格中与△ABC相似且面积最大的格点三角形的个数,并画出其中一个(不需证明).
| 5 |
| 5 |
(1)如图①,点M为AB的中点,在线段AC上取点N,使△AMN与△ABC相似,求线段MN的长;
(2)如图,是由100个边长为1的小正方形组成的10×10的正方形网格,设顶点在这些小正方形顶点的三角形为格点三角形.
①请你在所给的网格中画出格点△A1B1C1与△ABC全等(画出一个即可,不需证明);
②试直接写出所给的网格中与△ABC相似且面积最大的格点三角形的个数,并画出其中一个(不需证明).

考点:作图—相似变换
专题:
分析:(1)由于相似三角形的对应边不能确定,故应分△AMN∽△ABC与△ANM∽△ABC两种情况进行讨论;
(2)①在所给的网格中画出格点△A1B1C1与△ABC全等即可;
②根据相似三角形的性质画出最大的格点三角形即可.
(2)①在所给的网格中画出格点△A1B1C1与△ABC全等即可;
②根据相似三角形的性质画出最大的格点三角形即可.
解答: 解:(1)当△AMN∽△ABC时,
解:(1)当△AMN∽△ABC时,
∵点M为AB的中点,AB=
,AC=2
,BC=3,
∴
=
,
∴
=
=
,即
=
,解得MN=
;
当△ANM∽△ABC时,
∵
=
,即
=
=
,解得MN=
.
(2)①如图所示,△A1B1C1即为所求;
②共8个,如图所示△A2B2C2即为所求.
 解:(1)当△AMN∽△ABC时,
解:(1)当△AMN∽△ABC时,∵点M为AB的中点,AB=
| 5 |
| 5 |
∴
| AM |
| AB |
| 1 |
| 2 |
∴
| MN |
| BC |
| AM |
| AB |
| 1 |
| 2 |
| MN |
| 3 |
| 1 |
| 2 |
| 3 |
| 2 |
当△ANM∽△ABC时,
∵
| MN |
| BC |
| AM |
| AC |
| MN |
| 3 |
| ||
| AC |
| ||||
2
|
| 3 |
| 4 |
(2)①如图所示,△A1B1C1即为所求;
②共8个,如图所示△A2B2C2即为所求.
点评:本题考查的是作图-相似变换,熟知相似三角形的对应边成比例是解答此题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
△ABC的三边长分别为6、8、10,则其内切圆和外接圆的半径分别是( )
| A、2,5 | B、1,5 |
| C、4,5 | D、4,10 |
 如图,△ABC中,∠A=40°,BD、CE是角平分线,则∠BEC+∠BDC=( )
如图,△ABC中,∠A=40°,BD、CE是角平分线,则∠BEC+∠BDC=( )| A、130° | B、140° |
| C、150° | D、160° |
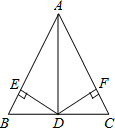 如图,已知AB=AC,D是BC的中点,DE⊥AB,DF⊥AC,DE=DF,求证:AD⊥BC.
如图,已知AB=AC,D是BC的中点,DE⊥AB,DF⊥AC,DE=DF,求证:AD⊥BC.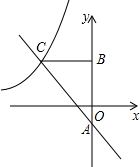 如图,一次函数y=kx-1(k≠0)的图象与反比例函数y=
如图,一次函数y=kx-1(k≠0)的图象与反比例函数y= 如图,已知线段a.
如图,已知线段a.