题目内容
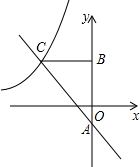 如图,一次函数y=kx-1(k≠0)的图象与反比例函数y=
如图,一次函数y=kx-1(k≠0)的图象与反比例函数y=| m |
| x |
(1)求AB的长;
(2)若AC=5,S△ABC=8,求m与k的值.
考点:反比例函数与一次函数的交点问题
专题:
分析:(1)求得一次函数与y轴的交点A的坐标,即可求得AB的长;
(2)根三角形的面积公式即可求得BC的长,则C的坐标即可求得,然后代入解析式求得m和k的值.
(2)根三角形的面积公式即可求得BC的长,则C的坐标即可求得,然后代入解析式求得m和k的值.
解答:解:(1)在y=kx-1中,令x=0,解得:y=-1.
则A的坐标是(0,-1).
则AB=4;
(2)设BC的长是m,则
×4m=8,
解得:m=4,
则C的坐标是(4,3);
把(4,3)代入y=
,得:3=
,解得:m=12;
把(4,3)代入y=kx-1得:4k-1=3,解得:k=1.
则A的坐标是(0,-1).
则AB=4;
(2)设BC的长是m,则
| 1 |
| 2 |
解得:m=4,
则C的坐标是(4,3);
把(4,3)代入y=
| m |
| x |
| m |
| 4 |
把(4,3)代入y=kx-1得:4k-1=3,解得:k=1.
点评:本题考查了待定系数法求函数的解析式,以及三角形的面积公式,正确求得C的坐标是关键.

练习册系列答案
 小天才课时作业系列答案
小天才课时作业系列答案 一课四练系列答案
一课四练系列答案 黄冈小状元满分冲刺微测验系列答案
黄冈小状元满分冲刺微测验系列答案 新辅教导学系列答案
新辅教导学系列答案 阳光同学一线名师全优好卷系列答案
阳光同学一线名师全优好卷系列答案
相关题目
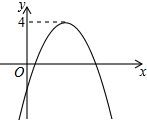 函数y=ax2+bx+c的图象如图所示,那么关于x的一元二次方程ax2+bx+c-4=0的根的情况是( )
函数y=ax2+bx+c的图象如图所示,那么关于x的一元二次方程ax2+bx+c-4=0的根的情况是( )| A、有两个不相等的实数根 |
| B、有两个异号的实数根 |
| C、有两个相等的实数根 |
| D、没有实数根 |
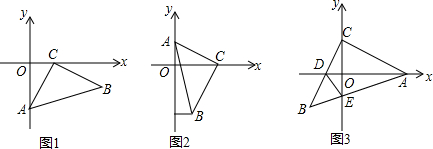
 如图,⊙O是△ACD的外接圆,AB是直径,过点D作直线DE∥AB,过点B作直线BE∥AD,两直线交于点E,如果∠ACD=45°,⊙O的半径是3cm.
如图,⊙O是△ACD的外接圆,AB是直径,过点D作直线DE∥AB,过点B作直线BE∥AD,两直线交于点E,如果∠ACD=45°,⊙O的半径是3cm.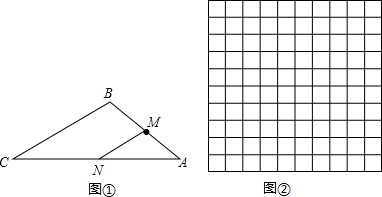
 如图,⊙O为Rt△ABC的内切圆,∠ACB=90°,若∠BOC=105°,AB=12cm,求BC的长.
如图,⊙O为Rt△ABC的内切圆,∠ACB=90°,若∠BOC=105°,AB=12cm,求BC的长.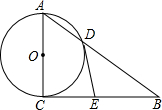 如图,在Rt△ABC中,∠ACB=90°,以AC为直径的⊙O与AB边交于点D,E为BC的中点,连接DE.
如图,在Rt△ABC中,∠ACB=90°,以AC为直径的⊙O与AB边交于点D,E为BC的中点,连接DE.