题目内容
已知等腰△ABC的底边c=3,另两边a,b恰好是关于x的方程x2-(2k+1)x+4(k-
)=0的两个根,求△ABC中a的边的长.
| 1 |
| 2 |
考点:一元二次方程的应用,等腰三角形的性质
专题:
分析:分c=3为腰和底两种情况,根据三角形三边关系定理及等腰三角形的特点,确定另两边的长即可.
解答:
解:当c=3为底边,则b,a为腰长,则b=a,则△=0.
∴(2k+1)2-4×4(k-
)=0,
解得:k1=k2=
.
此时原方程化为:x2-4x+4=0
∴x1=x2=2,即b=a=2.
当c=3为腰长,则32-3(2k+1)+4(k-
)=0,
解得:k=2,
此时原方程化为:x2-5x+6=0
∴x1=2,x2=3,即a=2或3.
综上所述:a的值为2或3.
∴(2k+1)2-4×4(k-
| 1 |
| 2 |
解得:k1=k2=
| 3 |
| 2 |
此时原方程化为:x2-4x+4=0
∴x1=x2=2,即b=a=2.
当c=3为腰长,则32-3(2k+1)+4(k-
| 1 |
| 2 |
解得:k=2,
此时原方程化为:x2-5x+6=0
∴x1=2,x2=3,即a=2或3.
综上所述:a的值为2或3.
点评:此题主要考查了根的判别式及三角形三边关系定理,注意求出三角形的三边后,要用三边关系定理检验.

练习册系列答案
相关题目
用代数式表示:“a与b的平方的和”正确的是( )
| A、a2+b2 |
| B、a+b |
| C、a+b |
| D、(a+b) |
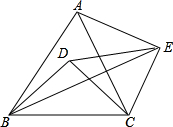 如图,△ABC和△EDC都是正三角形,连接BD、AE、BE,若∠AEB=45°,则∠DEB等于( )
如图,△ABC和△EDC都是正三角形,连接BD、AE、BE,若∠AEB=45°,则∠DEB等于( )| A、15° | B、20° |
| C、25° | D、30° |
下列命题中是真命题的是( )
| A、五边形的外角和等于360° |
| B、如果a+b>0,那么ab>0 |
| C、同位角相等 |
| D、一个锐角与一个钝角的和等于一个平角 |
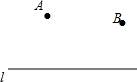 已知A,B两点在直线l的同侧,在直线l上求作一点P,使AP+BP的值最小.
已知A,B两点在直线l的同侧,在直线l上求作一点P,使AP+BP的值最小.