题目内容
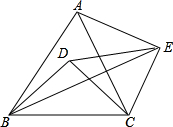 如图,△ABC和△EDC都是正三角形,连接BD、AE、BE,若∠AEB=45°,则∠DEB等于( )
如图,△ABC和△EDC都是正三角形,连接BD、AE、BE,若∠AEB=45°,则∠DEB等于( )| A、15° | B、20° |
| C、25° | D、30° |
考点:全等三角形的判定与性质,等边三角形的性质
专题:
分析:首先由△ABC和△EDC都是正三角形,易证得△BCD≌△ACE,然后由全等三角形的对应角相等,求得∠BDC+∠DEB=105°,又由在△DBE中,∠BDE+∠DEB+∠DBE=180°,即可求得答案.
解答:
解:∵△ABC和△EDC都是正三角形,
∴BC=AC,DC=EC,∠BCA=∠DCE=60°,
∴∠BCD=∠ACE,
在△BCD和△ACE中,
,
∴△BCD≌△ACE(SAS),
∴∠BDC=∠AEC=∠AEB+∠CED-∠DEB=45°+60°-∠DEB=105°-∠DEB,
∴∠BDC+∠DEB=105°,
∵在△DBE中,∠BDE+∠DEB+∠DBE=180°,
即∠BDC+∠CDE+∠DEB+∠DBE=180°,
∴∠DBE=180°-(∠BDC+∠CDE+∠DEB)=180°-105°-60°=15°.
故选A.
∴BC=AC,DC=EC,∠BCA=∠DCE=60°,
∴∠BCD=∠ACE,
在△BCD和△ACE中,
|
∴△BCD≌△ACE(SAS),
∴∠BDC=∠AEC=∠AEB+∠CED-∠DEB=45°+60°-∠DEB=105°-∠DEB,
∴∠BDC+∠DEB=105°,
∵在△DBE中,∠BDE+∠DEB+∠DBE=180°,
即∠BDC+∠CDE+∠DEB+∠DBE=180°,
∴∠DBE=180°-(∠BDC+∠CDE+∠DEB)=180°-105°-60°=15°.
故选A.
点评:此题考查了全等三角形的判定与性质.此题难度较大,注意掌握数形结合思想的应用.

练习册系列答案
相关题目
两圆的半径分别为3cm和4cm,且两圆的圆心距为7cm,则这两圆的公切线条数共有( )
| A、1条 | B、2条 | C、3条 | D、4条 |
2014年10月7日21时49分,云南省普洱市景谷发生6.6级地震,截至9日11时,地震造成普洱市、临沧市共12个县区30.88万人不同程度受灾,为支援灾区,某市向普洱市派出11组医疗救援队(每组6人)和12组搜救队(每组15人),后因余震,从派去普洱市的医疗救援队和搜救队中各抽出5组派往临沧市,则从该市派去参加救援的人在普洱市还剩( )
| A、151人 | B、141人 |
| C、131人 | D、105人 |
下列现象不属于平移现象的是( )
| A、小花乘电梯从一楼到十楼 |
| B、足球在操场上直线滚动 |
| C、一个铁球从高空落下(球不旋转) |
| D、小朋友坐滑梯下滑 |
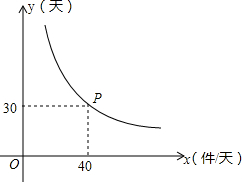 问题情境:为了提高产品的技术含量,我省某贸易公司计划把研发的一批新产品精加工后再投放市场,加工所需时间y(单位:天)与平均每天的工作量x(单位:件/天)之间的关系是我们学过的某种函数,其图象如图所示.
问题情境:为了提高产品的技术含量,我省某贸易公司计划把研发的一批新产品精加工后再投放市场,加工所需时间y(单位:天)与平均每天的工作量x(单位:件/天)之间的关系是我们学过的某种函数,其图象如图所示.
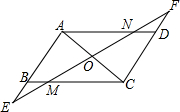 如图,已知:AB=DC,AD=BC.
如图,已知:AB=DC,AD=BC.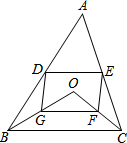 D、E分别是不等边三角形ABC(即AB≠BC≠AC)的边AB、AC的中点,O是△ABC所在平面上的动点,连接OB、OC,点G、F分别是OB、OC的中点,顺次连接点D、G、F、E.
D、E分别是不等边三角形ABC(即AB≠BC≠AC)的边AB、AC的中点,O是△ABC所在平面上的动点,连接OB、OC,点G、F分别是OB、OC的中点,顺次连接点D、G、F、E.