题目内容
甲口袋有2个相同的小球,它们分别写有数字1和2,;乙口袋中装有3个相同的小球,它们分别写有数字3、4、5,从这两个口袋中各随机地取出1个球.
(1)用“树状图法”或“列表法”表示所有可能出现的结果;
(2)取出的两个小球上所写数字之和是偶数的概率是多少?
(1)用“树状图法”或“列表法”表示所有可能出现的结果;
(2)取出的两个小球上所写数字之和是偶数的概率是多少?
考点:列表法与树状图法
专题:
分析:(1)首先根据题意画出树状图,然后由树状图求得所有等可能的结果;
(2)由(1)中的树状图求得取出的两个小球上所写数字之和是偶数的情况,再利用概率公式即可求得答案.
(2)由(1)中的树状图求得取出的两个小球上所写数字之和是偶数的情况,再利用概率公式即可求得答案.
解答:
解:(1)画树状图得:

则共有6种等可能的结果;
(2)∵取出的两个小球上所写数字之和是偶数的有3种情况,
∴取出的两个小球上所写数字之和是偶数的概率是:
=
.

则共有6种等可能的结果;
(2)∵取出的两个小球上所写数字之和是偶数的有3种情况,
∴取出的两个小球上所写数字之和是偶数的概率是:
| 3 |
| 6 |
| 1 |
| 2 |
点评:此题考查了树状图法与列表法求概率.用到的知识点为:概率=所求情况数与总情况数之比.

练习册系列答案
相关题目
把(-2)2014+(-2)2015分解因式的结果是( )
| A、22015 |
| B、-22015 |
| C、-22014 |
| D、22014 |
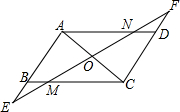 如图,已知:AB=DC,AD=BC.
如图,已知:AB=DC,AD=BC.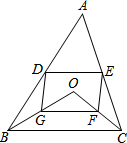 D、E分别是不等边三角形ABC(即AB≠BC≠AC)的边AB、AC的中点,O是△ABC所在平面上的动点,连接OB、OC,点G、F分别是OB、OC的中点,顺次连接点D、G、F、E.
D、E分别是不等边三角形ABC(即AB≠BC≠AC)的边AB、AC的中点,O是△ABC所在平面上的动点,连接OB、OC,点G、F分别是OB、OC的中点,顺次连接点D、G、F、E.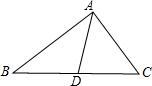 如图所示,在△ABC中,AB>AC,AD是△ABC的角平分线,请比较AB-AC与BD-DC的大小,并说明理由.
如图所示,在△ABC中,AB>AC,AD是△ABC的角平分线,请比较AB-AC与BD-DC的大小,并说明理由.