题目内容
18.(1)3(x-3)2=3-x(2)x2-2x=2x+1.
分析 (1)提取公因式(x-3)即可得到(x-3)(3x-8)=0,再解两个一元一次方程即可;
(2)首先合并同类项,然后进行配方,进而开方求出方程的根.
解答 解:(1)∵3(x-3)2=3-x,
∴(x-3)(3x-8)=0,
∴x-3=0或3x-8=0,
∴x1=3,x2=$\frac{8}{3}$;
(2)∵x2-2x=2x+1,
∴x2-4x-1=0,
∴(x-2)2=5,
∴x-2=±$\sqrt{5}$,
∴x1=2+$\sqrt{5}$,x2=2-$\sqrt{5}$.
点评 本题考查了一元二次方程的解法.解一元二次方程常用的方法有直接开平方法,配方法,公式法,因式分解法,要根据方程的特点灵活选用合适的方法.

练习册系列答案
相关题目
3. 反比例函数y1=$\frac{4}{x}$、y2=$\frac{k}{x}$(k≠0)在第一象限的图象如图,过y1上的任意一点A,作x轴的平行线交y2于B,交y轴于C.若S△AOB=1,则k=( )
反比例函数y1=$\frac{4}{x}$、y2=$\frac{k}{x}$(k≠0)在第一象限的图象如图,过y1上的任意一点A,作x轴的平行线交y2于B,交y轴于C.若S△AOB=1,则k=( )
 反比例函数y1=$\frac{4}{x}$、y2=$\frac{k}{x}$(k≠0)在第一象限的图象如图,过y1上的任意一点A,作x轴的平行线交y2于B,交y轴于C.若S△AOB=1,则k=( )
反比例函数y1=$\frac{4}{x}$、y2=$\frac{k}{x}$(k≠0)在第一象限的图象如图,过y1上的任意一点A,作x轴的平行线交y2于B,交y轴于C.若S△AOB=1,则k=( )| A. | 7 | B. | 6 | C. | 5 | D. | 3 |
10.方程组的$\left\{\begin{array}{l}{x+y=6}\\{x-y=4}\end{array}\right.$解为( )
| A. | $\left\{\begin{array}{l}{x=2}\\{y=4}\end{array}\right.$ | B. | $\left\{\begin{array}{l}{x=3}\\{y=3}\end{array}\right.$ | C. | $\left\{\begin{array}{l}{x=4}\\{y=2}\end{array}\right.$ | D. | $\left\{\begin{array}{l}{x=5}\\{y=1}\end{array}\right.$ |
 如图所示,P为△ABC内一点.
如图所示,P为△ABC内一点.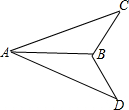 如图,已知AB平分∠CAD,AC=AD.求证:∠C=∠D.
如图,已知AB平分∠CAD,AC=AD.求证:∠C=∠D.