题目内容
12．
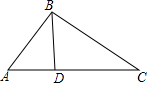如图，在△ABC中，D是AC上一点，联结BD，∠CBD=∠A．（1）求证：△CBD∽△CAB；
（2）若D是AC中点，CD=3，求BC的长．
分析 （1）根据∠CBD=∠A，∠C是公共角即可得出结论；
（2）根据（1）中△CBD∽△CAB即可得出结论．
解答 （1）证明：∵∠CBD=∠A，∠C是公共角，
∴△CBD∽△CAB；
（2）解：∵D是AC中点，CD=3，
∴AC=2AD=6．
∵△CBD∽△CAB，
∴$\frac{BC}{AC}$=$\frac{CD}{BC}$，即BC2=AC•CD=6×3=18，
∴BC=3$\sqrt{2}$．
点评 本题考查的是相似三角形的判定与性质，熟知相似三角形的对应边成比例是解答此题的关键．
练习册系列答案
导学教程高中新课标系列答案
小学课时特训系列答案
相关题目
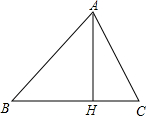已知：如图，在△ABC中，∠ABC=45°，AH⊥BC于点H，点D为AH上的一点，且DH=HC，连结BD并延长BD交AC于点E，连结EH．
如图，四边形ABCD为正方形，点A坐标为（0，1），点B坐标为（0，-2），反比例函数y=$\frac{k}{x}$的图象经过点C，一次函数y=ax+b的图象经过A、C两点．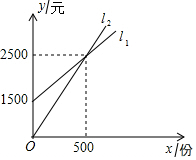
某公司要印制产品宣传材料，l1反映了甲印刷厂的收费y1（元）与印制数量x（份）间的关系，l2反映了乙印刷厂的收费y2（元）与印制数量x（份）间的关系．