题目内容
12.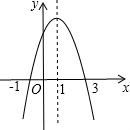 结合二次函数y=-$\frac{2}{3}$x2+$\frac{4}{3}$x+2的图象图回答:
结合二次函数y=-$\frac{2}{3}$x2+$\frac{4}{3}$x+2的图象图回答:(1)当x=-1或3时,y=0
(2)当-1<x<3时,y>0
(3)当x<-1或x>3时,y<0.
分析 (1)直接根据函数的图象与x轴的交点分别为(-1,0),(0,3)可得出结论;
(2)根据当-1<x<3时,函数图象在x轴的上方可得出结论;
(3)根据当x<-1或x>3时,函数图象在x轴下方可得出结论.
解答 解:(1)∵函数的图象与x轴的交点分别为(-1,0),(3,0),
∴当x=-1或x=3时,y=0.
故答案为:-1或3;
(2)∵由函数图象可知,当-1<x<3时,函数图象在x轴的上方,
∴当-1<x<3时,y>0.
故答案为:-1<x<3;
(3)∵由函数图象可知,当x<-1或x>3时函数图象在x轴下方,
∴当x<-1或x>3时,y<0.
故答案为:x<-1或x>3.
点评 本题考查的是二次函数与不等式,能根据函数图象利用数形结合求出不等式的解是解答此题的关键.

练习册系列答案
 新非凡教辅冲刺100分系列答案
新非凡教辅冲刺100分系列答案
相关题目
4.根据表中二次函数y=ax2+bx+c的自变量x与函数值y的对应值,判断一元二次方程ax2+bx+c=0的一个根x的取值范围是( )
| x | 617 | 618 | 619 | 620 |
| y | -0.03 | -0.01 | 0.02 | 0.04 |
| A. | 6<x<617 | B. | 617<x<618 | C. | 618<x<619 | D. | 619<x<7 |

 把下列各数在数轴上表示出来.-2$\frac{1}{2}$,0,-1,1,|-3$\frac{1}{2}$|
把下列各数在数轴上表示出来.-2$\frac{1}{2}$,0,-1,1,|-3$\frac{1}{2}$|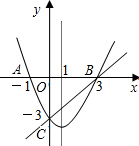 如图,在同一直角坐标系中,二次函数的图象与两坐标轴分别交于A(-1,0)、点B(3,0)和点C(0,-3),一次函数的图象与抛物线交于B、C两点.
如图,在同一直角坐标系中,二次函数的图象与两坐标轴分别交于A(-1,0)、点B(3,0)和点C(0,-3),一次函数的图象与抛物线交于B、C两点.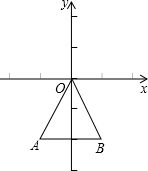 如图,△OAB三个顶点的坐标分别为O(0,0)、A(-1,-2)、B(1,-2),以B点为位似中心将△OAB放大2倍,求放大后的三角形各顶点的坐标.(提示:分两种情况)
如图,△OAB三个顶点的坐标分别为O(0,0)、A(-1,-2)、B(1,-2),以B点为位似中心将△OAB放大2倍,求放大后的三角形各顶点的坐标.(提示:分两种情况)