题目内容
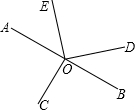 如图,点O是直线AB上的一点,OC平分∠AOB,在直线AB另一端以O为顶点作∠DOE=90°.
如图,点O是直线AB上的一点,OC平分∠AOB,在直线AB另一端以O为顶点作∠DOE=90°.(1)若∠AOE=48°,求∠BOD的度数;
(2)写出图中与∠AOE互余的角;
(3)∠AOE与∠COD有什么数量关系?请写出你的结论并说明理由.
考点:余角和补角,角平分线的定义
专题:
分析:(1)∠BOD=180°-∠AOE-DOE=42°;
(2)由∠AOE+∠BOD=90°,得出与∠AOE互余的角是∠BOD;
(3)先求出∠BOC=90°,再由∠AOE+∠BOD=90°,得出∠AOE+∠COD=180°.
(2)由∠AOE+∠BOD=90°,得出与∠AOE互余的角是∠BOD;
(3)先求出∠BOC=90°,再由∠AOE+∠BOD=90°,得出∠AOE+∠COD=180°.
解答:解:(1)∵∠AOE=48°,∠DOE=90°,
∴∠BOD=180°-90°-48°=42°;
(2)∵∠DOE=90°,
∴∠AOE+∠BOD=180°-90°=90°,
∴∠DOB与∠AOE互余,
∴图中与∠AOE互余的角是∠BOD;
(3)∠AOE+∠COD=180°;理由如下:
∵OC平分∠AOB,
∴∠AOC=∠BOC=90°,
∵∠AOB=180°,∠DOE=90°,
∴∠AOE+∠BOD=90°,
∴∠AOE+∠COD=∠AOE+∠BOD+∠BOC=90°+90°=180°.
∴∠BOD=180°-90°-48°=42°;
(2)∵∠DOE=90°,
∴∠AOE+∠BOD=180°-90°=90°,
∴∠DOB与∠AOE互余,
∴图中与∠AOE互余的角是∠BOD;
(3)∠AOE+∠COD=180°;理由如下:
∵OC平分∠AOB,
∴∠AOC=∠BOC=90°,
∵∠AOB=180°,∠DOE=90°,
∴∠AOE+∠BOD=90°,
∴∠AOE+∠COD=∠AOE+∠BOD+∠BOC=90°+90°=180°.
点评:本题考查了余角和补角以及角平分线的定义;弄清各个角之间的关系是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
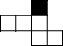
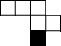
 如图,它需再添一个面,折叠后才能围成一个正方体.图中的黑色小正方形分别由四位同学补画,其中正确的是( )
如图,它需再添一个面,折叠后才能围成一个正方体.图中的黑色小正方形分别由四位同学补画,其中正确的是( )

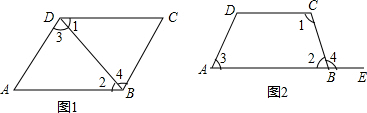
 如图,图中内错角有
如图,图中内错角有 如图,点P是菱形ABCD的对角线BD上一点,连结CP并延长,交AD于E,交BA的延长线于点F.试问:
如图,点P是菱形ABCD的对角线BD上一点,连结CP并延长,交AD于E,交BA的延长线于点F.试问: