题目内容
12. 一个正方形和两个等边三角形的位置如图所示,若∠1=40°,则∠2+∠3=110°.
一个正方形和两个等边三角形的位置如图所示,若∠1=40°,则∠2+∠3=110°.
分析 设围成的小三角形为△ABC,分别用∠1、∠2、∠3表示出△ABC的三个内角,再利用三角形的内角和等于180°列式整理即可得解.
解答  解:如图,∠BAC=180°-90°-∠1=90°-∠1,
解:如图,∠BAC=180°-90°-∠1=90°-∠1,
∠ABC=180°-60°-∠3=120°-∠3,
∠ACB=180°-60°-∠2=120°-∠2,
在△ABC中,∠BAC+∠ABC+∠ACB=180°,
∴90°-∠1+120°-∠3+120°-∠2=180°,
∴∠1+∠2=150°-∠3,
∵∠1=40°,
∴∠2+∠3=150°-40°=110°.
故答案为:110°.
点评 本题考查了三角形的内角和定理,用∠1、∠2、∠3表示出△ABC的三个内角是解题的关键,也是本题的难点.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
7.下列各数中比0小的数是( )
| A. | -2 | B. | 1$\frac{1}{3}$ | C. | 3 | D. | $\sqrt{3}$ |
17.一个圆锥的侧面展开图是半径为8cm,圆心角为120°的扇形,则这个圆锥的底面半径为( )
| A. | $\frac{16}{3}\sqrt{2}$ | B. | $\frac{16}{3}$cm | C. | $\frac{8}{3}\sqrt{2}$cm | D. | $\frac{8}{3}$cm |
2. 象棋在中国有着三千多年的历史,由于用具简单,趣味性强,成为流行极为广泛的益智游戏.如图,是一局象棋残局,已知表示棋子“車”的点的坐标为(-2,1),棋子“炮”的点的坐标为(1,3),则表示棋子“馬”的点的坐标为( )
象棋在中国有着三千多年的历史,由于用具简单,趣味性强,成为流行极为广泛的益智游戏.如图,是一局象棋残局,已知表示棋子“車”的点的坐标为(-2,1),棋子“炮”的点的坐标为(1,3),则表示棋子“馬”的点的坐标为( )
 象棋在中国有着三千多年的历史,由于用具简单,趣味性强,成为流行极为广泛的益智游戏.如图,是一局象棋残局,已知表示棋子“車”的点的坐标为(-2,1),棋子“炮”的点的坐标为(1,3),则表示棋子“馬”的点的坐标为( )
象棋在中国有着三千多年的历史,由于用具简单,趣味性强,成为流行极为广泛的益智游戏.如图,是一局象棋残局,已知表示棋子“車”的点的坐标为(-2,1),棋子“炮”的点的坐标为(1,3),则表示棋子“馬”的点的坐标为( )| A. | (-4,3) | B. | (3,4) | C. | (-3,4) | D. | (4,3) |
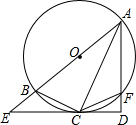 如图,已知AB为⊙O的直径,F为⊙O上一点,AC平分∠BAF且交⊙O于点C,过点C作CD⊥AF于点D,延长AB、DC交于点E,连接BC、CF.
如图,已知AB为⊙O的直径,F为⊙O上一点,AC平分∠BAF且交⊙O于点C,过点C作CD⊥AF于点D,延长AB、DC交于点E,连接BC、CF.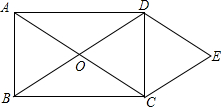 如图,矩形ABCD的对角线AC、BD相交于点O,DE∥AC,CE∥BD.
如图,矩形ABCD的对角线AC、BD相交于点O,DE∥AC,CE∥BD.