题目内容
18. 如图,在矩形ABCD中,对角线AC,BD相交于点O,AB=4,∠AOD=120°,求AC的长.
如图,在矩形ABCD中,对角线AC,BD相交于点O,AB=4,∠AOD=120°,求AC的长.
分析 由矩形的性质得出OA=OB,再证明△AOB是等边三角形,得出OA=AB=4,即可求出AC的长.
解答 解:∵四边形ABCD是矩形,
∴OA=OC=$\frac{1}{2}$AC,OB=OD=$\frac{1}{2}$BD,AC=BD,
∴OA=OB,
∵∠AOD=120°,
∴∠AOB=60°,
∴△AOB是等边三角形,
∴OA=AB=4,
∴AC=2OA=8.
点评 本题考查了矩形的性质、等边三角形的判定与性质;熟练掌握矩形的性质,证明三角形是等边三角形是解决问题的关键.

练习册系列答案
 中考利剑中考试卷汇编系列答案
中考利剑中考试卷汇编系列答案
相关题目
10.方程x2=x的根是( )
| A. | x=1 | B. | x=0 | C. | x1=0或x2=1 | D. | x1=-1或x2=11 |
8.数1,$\frac{3}{4}$,$\frac{5}{9}$,$\frac{7}{16}$,$\frac{9}{25}$…按此规律写下去,那么第n(n为正整数)个数是( )
| A. | $\frac{2n+1}{{n}^{2}}$ | B. | $\frac{2n-1}{n}$ | C. | $\frac{2n-1}{{n}^{2}}$ | D. | $\frac{n-4}{{n}^{2}}$ |
 如图,在面积为21cm2的矩形ABCD中,DE平分∠ADC交BC于点E,EF⊥AD交AD于点F,若EF=3,则AE=5cm.
如图,在面积为21cm2的矩形ABCD中,DE平分∠ADC交BC于点E,EF⊥AD交AD于点F,若EF=3,则AE=5cm.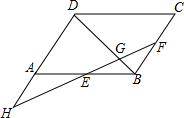 如图所示,在?ABCD中,E为AB中点,在BC上取一点F,使BF:FC=1:2,连接EF交DA的延长线于H,交BD于G.试说明:BD=5BG.
如图所示,在?ABCD中,E为AB中点,在BC上取一点F,使BF:FC=1:2,连接EF交DA的延长线于H,交BD于G.试说明:BD=5BG. 如图,沿AC方向开山修路,为了加快施工进度,要在山的另一面同时施工,工人师傅在AC上取一点B,在小山外取一点D,连接BD并延长,使DF=BD,过F点作AE的平行线FM,交ED的延长线于点M,测量FM的长就是BE的长,你知道其中的道理吗?
如图,沿AC方向开山修路,为了加快施工进度,要在山的另一面同时施工,工人师傅在AC上取一点B,在小山外取一点D,连接BD并延长,使DF=BD,过F点作AE的平行线FM,交ED的延长线于点M,测量FM的长就是BE的长,你知道其中的道理吗?