题目内容
 如图,在⊙O的弦AB的长等于⊙O的半径,求∠ACB的度数.
如图,在⊙O的弦AB的长等于⊙O的半径,求∠ACB的度数.考点:圆周角定理,等边三角形的判定与性质
专题:
分析:由弦AB的长等于⊙O的半径,可得△AOB为等边三角形,且∠AOB=60°,在优弧AB上任找一点D,连接AD,BD,根据圆周角定理可得∠D=
∠AOB=30°,然后再根据圆内接四边形的性质,可求∠ACB的度数.
| 1 |
| 2 |
解答:解:在优弧AB上任找一点D,连接AD,BD,

∵弦AB的长等于⊙O的半径,
∴△AOB为等边三角形,
∴∠AOB=60°,
由圆周角定理可得:
∠D=
∠AOB=30°,
∵∠D+∠ACB=180°,
∴∠ACB=150°.

∵弦AB的长等于⊙O的半径,
∴△AOB为等边三角形,
∴∠AOB=60°,
由圆周角定理可得:
∠D=
| 1 |
| 2 |
∵∠D+∠ACB=180°,
∴∠ACB=150°.
点评:此题考查了圆周角定理及圆内接四边形的性质,解题的关键是:添加辅助线,构造圆内接四边形.

练习册系列答案
相关题目
 如图,下面三个正方体的六个面都按相同规律涂有红、黄、蓝、白、黑、绿六种颜色,那么涂红色对面是( )
如图,下面三个正方体的六个面都按相同规律涂有红、黄、蓝、白、黑、绿六种颜色,那么涂红色对面是( )| A、黄色 | B、黑色 | C、蓝色 | D、绿色 |
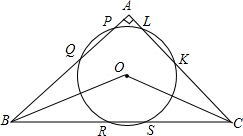 如图,在△ABC中,∠A为直角,⊙O与三角形三边交于点P、Q、R、S、K、L,若PQ=RS=KL,求∠BOC的大小.
如图,在△ABC中,∠A为直角,⊙O与三角形三边交于点P、Q、R、S、K、L,若PQ=RS=KL,求∠BOC的大小.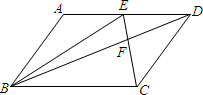 如图,平行四边形ABCD中,E为AD上的任意一点,三角形EFD的面积为4.5平方厘米,三角形BEF的面积为7.5平方厘米,则三角形ABE的面积为
如图,平行四边形ABCD中,E为AD上的任意一点,三角形EFD的面积为4.5平方厘米,三角形BEF的面积为7.5平方厘米,则三角形ABE的面积为 如图,已知∠A+∠DBA=180°,∠3=58°,求∠4的度数.
如图,已知∠A+∠DBA=180°,∠3=58°,求∠4的度数. 如图,∠B=∠D,∠1=∠2.试说明:AB∥CD.
如图,∠B=∠D,∠1=∠2.试说明:AB∥CD. 如图,在平面直角坐标系中,△ABC的三个顶点坐标分别为A(-2,1),B(-1,4),C(-3,2).
如图,在平面直角坐标系中,△ABC的三个顶点坐标分别为A(-2,1),B(-1,4),C(-3,2).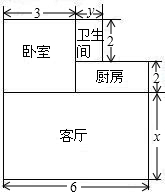 小亮家购买了一套保障房,准备将地面铺上地砖,地面结构如图所示,根据图中的数据(单位:m),解答下列问题:
小亮家购买了一套保障房,准备将地面铺上地砖,地面结构如图所示,根据图中的数据(单位:m),解答下列问题: