题目内容
3.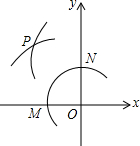 如图,在平面直角坐标系中,以点O为圆心,适当长为半径画弧,交x轴于点M,交y轴于点N,再分别以点M、N为圆心,大于$\frac{1}{2}$MN的长为半径画弧,两弧在第二象限交于点P,若点P的坐标为(6a,2b-1),则a和b的数量关系为( )
如图,在平面直角坐标系中,以点O为圆心,适当长为半径画弧,交x轴于点M,交y轴于点N,再分别以点M、N为圆心,大于$\frac{1}{2}$MN的长为半径画弧,两弧在第二象限交于点P,若点P的坐标为(6a,2b-1),则a和b的数量关系为( )| A. | 6a-2b=1 | B. | 6a+2b=1 | C. | 6a-b=1 | D. | 6a+b=1 |
分析 根据作图方法可得点P在第二象限的角平分线上,根据角平分线的性质和第二象限内点的坐标符号可得6a+2b-1=0,然后再整理可得答案.
解答 解:根据作图方法可得点P在第二象限角平分线上;点P到x轴、y轴的距离相等;点P的横纵坐标互为相反数,
则P点横纵坐标的和为0,
故6a+2b-1=0(或-6a=2b-1),
整理得:6a+2b=1,
故选B.
点评 此题主要考查了基本作图-角平分线的做法以及坐标与图形的性质:点到坐标轴的距离与这个点的坐标是有区别的,表现在两个方面:①到x轴的距离与纵坐标有关,到y轴的距离与横坐标有关;②距离都是非负数,而坐标可以是负数,在由距离求坐标时,需要加上恰当的符号.

练习册系列答案
相关题目
14.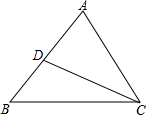 如图,给出下列条件,其中不能单独判定△ABC∽△ACD的条件为( )
如图,给出下列条件,其中不能单独判定△ABC∽△ACD的条件为( )
 如图,给出下列条件,其中不能单独判定△ABC∽△ACD的条件为( )
如图,给出下列条件,其中不能单独判定△ABC∽△ACD的条件为( )| A. | ∠B=∠ACD | B. | ∠ADC=∠ACB | C. | $\frac{AC}{CD}$=$\frac{AB}{BC}$ | D. | $\frac{AC}{AD}$=$\frac{AB}{AC}$ |
8.下列运算正确的是( )
| A. | a2•a3=a6 | B. | (a2)3=a6 | C. | a6÷a2=a3 | D. | 23=6 |
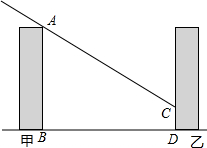 有一朝向为正南方向的楼,该楼的一楼是高5米的小区超市,超市以上是居民区,在该楼的前面20米处要盖一栋高16米的甲楼,当冬季正午的阳光与水平线的夹角为32°时.
有一朝向为正南方向的楼,该楼的一楼是高5米的小区超市,超市以上是居民区,在该楼的前面20米处要盖一栋高16米的甲楼,当冬季正午的阳光与水平线的夹角为32°时.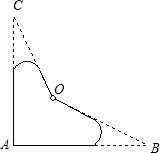 一个零件的形状如图所示,按规定∠A,∠B,∠C的度数应为90°,21°,32°,产品检验员用工具测得∠BOC=140°,就判定这个零件不合格,为什么?
一个零件的形状如图所示,按规定∠A,∠B,∠C的度数应为90°,21°,32°,产品检验员用工具测得∠BOC=140°,就判定这个零件不合格,为什么?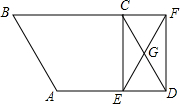 如图,点E是平行四边形ABCD边AD上的一点,点G是CD的中点,连接EG并延长,交BC延长线于F,连接CE、DF.求证:四边形CEDF是平行四边形.
如图,点E是平行四边形ABCD边AD上的一点,点G是CD的中点,连接EG并延长,交BC延长线于F,连接CE、DF.求证:四边形CEDF是平行四边形.