题目内容
14.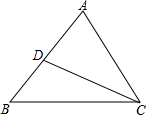 如图,给出下列条件,其中不能单独判定△ABC∽△ACD的条件为( )
如图,给出下列条件,其中不能单独判定△ABC∽△ACD的条件为( )| A. | ∠B=∠ACD | B. | ∠ADC=∠ACB | C. | $\frac{AC}{CD}$=$\frac{AB}{BC}$ | D. | $\frac{AC}{AD}$=$\frac{AB}{AC}$ |
分析 根据相似三角形的判定定理对各个选项逐一分析即可.
解答 解:∵∠A是公共角,
∴再加上∠B=∠ACD,或∠ADC=∠ACB都可判定△ABC∽△ACD,
∵∠A是公共角,再加上AC2=AD•AB,即 $\frac{AC}{AD}=\frac{AB}{AC}$,也可判定△ABC∽△ACD,
∴选项A、B、D都可判定△ABC∽△ACD.
而选项C中的对两边成比例,但不是相应的夹角相等,所以选项C不能.
故选C.
点评 本题考查了相似三角形的判定,此题主要考查学生对相似三角形判定定理的理解和掌握,难度不大,属于基础题,要求学生应熟练掌握.

练习册系列答案
 口算题天天练系列答案
口算题天天练系列答案
相关题目
5.直角坐标系中,P点在第四象限,则P点的坐标可能是( )
| A. | (6,-4) | B. | (5,2) | C. | (-3,-6) | D. | (-3,4) |
19.(2×102)3=( )
| A. | 2×106 | B. | 5×106 | C. | 8×106 | D. | 8×102 |
3.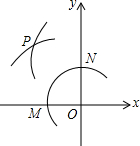 如图,在平面直角坐标系中,以点O为圆心,适当长为半径画弧,交x轴于点M,交y轴于点N,再分别以点M、N为圆心,大于$\frac{1}{2}$MN的长为半径画弧,两弧在第二象限交于点P,若点P的坐标为(6a,2b-1),则a和b的数量关系为( )
如图,在平面直角坐标系中,以点O为圆心,适当长为半径画弧,交x轴于点M,交y轴于点N,再分别以点M、N为圆心,大于$\frac{1}{2}$MN的长为半径画弧,两弧在第二象限交于点P,若点P的坐标为(6a,2b-1),则a和b的数量关系为( )
 如图,在平面直角坐标系中,以点O为圆心,适当长为半径画弧,交x轴于点M,交y轴于点N,再分别以点M、N为圆心,大于$\frac{1}{2}$MN的长为半径画弧,两弧在第二象限交于点P,若点P的坐标为(6a,2b-1),则a和b的数量关系为( )
如图,在平面直角坐标系中,以点O为圆心,适当长为半径画弧,交x轴于点M,交y轴于点N,再分别以点M、N为圆心,大于$\frac{1}{2}$MN的长为半径画弧,两弧在第二象限交于点P,若点P的坐标为(6a,2b-1),则a和b的数量关系为( )| A. | 6a-2b=1 | B. | 6a+2b=1 | C. | 6a-b=1 | D. | 6a+b=1 |
 如图,若AE是△ABC的中线,BC=4,则BE=2.
如图,若AE是△ABC的中线,BC=4,则BE=2.