题目内容
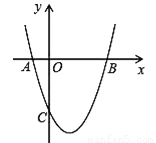
如图,抛物线y=x2 +bx+c与x轴交于A(﹣1,0),B(3,0)两点.
(1)求该抛物线的解析式;
(2)求该抛物线的对称轴以及顶点坐标;
(3)设(1)中的抛物线上有一个动点P,当点P在该抛物线上滑动到什么位置时,满足S△PAB=8,并求出此时P点的坐标.

 (1)y=x2﹣2x﹣3;(2)抛物线的对称轴x=1,顶点坐标(1,﹣4);(3)(,4)或(,4)或(1,﹣4).
【解析】试题分析:(1)由于抛物线y=x2+bx+c与x轴交于A(﹣1,0),B(3,0)两点,那么可以得到方程x2+bx+c=0的两根为x=﹣1或x=3,然后利用根与系数即可确定b、c的值.
(2)根据S△PAB=8,求得P的纵坐标,把纵坐标代入抛物线的解析式即可求得...
(1)y=x2﹣2x﹣3;(2)抛物线的对称轴x=1,顶点坐标(1,﹣4);(3)(,4)或(,4)或(1,﹣4).
【解析】试题分析:(1)由于抛物线y=x2+bx+c与x轴交于A(﹣1,0),B(3,0)两点,那么可以得到方程x2+bx+c=0的两根为x=﹣1或x=3,然后利用根与系数即可确定b、c的值.
(2)根据S△PAB=8,求得P的纵坐标,把纵坐标代入抛物线的解析式即可求得...
 英语小英雄天天默写系列答案
英语小英雄天天默写系列答案 暑假作业安徽少年儿童出版社系列答案
暑假作业安徽少年儿童出版社系列答案如图,抛物线y=x2 +bx+c与x轴交于A(﹣1,0),B(3,0)两点.
(1)求该抛物线的解析式;
(2)求该抛物线的对称轴以及顶点坐标;
(3)设(1)中的抛物线上有一个动点P,当点P在该抛物线上滑动到什么位置时,满足S△PAB=8,并求出此时P点的坐标.
 (1)y=x2﹣2x﹣3;(2)抛物线的对称轴x=1,顶点坐标(1,﹣4);(3)(,4)或(,4)或(1,﹣4).
【解析】试题分析:(1)由于抛物线y=x2+bx+c与x轴交于A(﹣1,0),B(3,0)两点,那么可以得到方程x2+bx+c=0的两根为x=﹣1或x=3,然后利用根与系数即可确定b、c的值.
(2)根据S△PAB=8,求得P的纵坐标,把纵坐标代入抛物线的解析式即可求得...
(1)y=x2﹣2x﹣3;(2)抛物线的对称轴x=1,顶点坐标(1,﹣4);(3)(,4)或(,4)或(1,﹣4).
【解析】试题分析:(1)由于抛物线y=x2+bx+c与x轴交于A(﹣1,0),B(3,0)两点,那么可以得到方程x2+bx+c=0的两根为x=﹣1或x=3,然后利用根与系数即可确定b、c的值.
(2)根据S△PAB=8,求得P的纵坐标,把纵坐标代入抛物线的解析式即可求得... 三角形的一边上有一点,它到三个顶点的距离相等,则这个三角形是_______三角形.
 直角
【解析】∵直角三角形斜边上的中线等于斜边的一半,
∴这个三角形是直角三角形.
故答案为:直角.
直角
【解析】∵直角三角形斜边上的中线等于斜边的一半,
∴这个三角形是直角三角形.
故答案为:直角. 如图,在一块边长为a的正方形纸板四周,各剪去一个边长为b(b<0)的正方形.
(1)用代数式表示阴影部分的面积;
(2)利用因式分解的方法计算当a=15.4,b=3.7时,阴影部分的面积.

 (1) a2-4b²;(2) 182.4.
【解析】试题分析:
试题解析:(1)用大正方形的面积减去四个小正方形的面积即可求得阴影部分的面积;(2)把所得的代数式用平方差公式因式分解后,代入求值即可.
(1)S阴影=a2-4b2;
(2)S阴影=(a+2b)(a-2b)=(15.4+2×3.7)(15.4-2×3.7)=22.8×8=182.4.
(1) a2-4b²;(2) 182.4.
【解析】试题分析:
试题解析:(1)用大正方形的面积减去四个小正方形的面积即可求得阴影部分的面积;(2)把所得的代数式用平方差公式因式分解后,代入求值即可.
(1)S阴影=a2-4b2;
(2)S阴影=(a+2b)(a-2b)=(15.4+2×3.7)(15.4-2×3.7)=22.8×8=182.4. 已知a,b,c为△ABC三边长,且满足a2c2-b2c2=a4-b4,则它的形状为( )
A. 直角三角形 B. 等腰三角形 C. 等腰直角三角形 D. 等腰三角形或直角三角形
 D
【解析】试题分析:由a2c2-b2c2=a4-b4,得
a4+b2c2-a2c2-b4=(a4-b4)+(b2c2-a2c2)=(a2+b2)(a2-b2)-c2(a2-b2)=(a2-b2)(a2+b2-c2)=(a+b)(a-b)(a2+b2-c2)=0,
∵a+b>0,∴a-b=0或a2+b2-c2=0,
即a=b或a2+b2=c2,则△ABC为等腰三角形或直角三...
D
【解析】试题分析:由a2c2-b2c2=a4-b4,得
a4+b2c2-a2c2-b4=(a4-b4)+(b2c2-a2c2)=(a2+b2)(a2-b2)-c2(a2-b2)=(a2-b2)(a2+b2-c2)=(a+b)(a-b)(a2+b2-c2)=0,
∵a+b>0,∴a-b=0或a2+b2-c2=0,
即a=b或a2+b2=c2,则△ABC为等腰三角形或直角三... 已知函数y=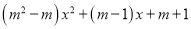
(1)若这个函数是一次函数,求m的值;
(2)若这个函数是二次函数,则m的值应怎样?
 (1)、m=0;(2)、m≠0且m≠1.
【解析】试题分析:(1)由一次函数的定义求解;
(2)由二次函数的定义求解.
试题解析:(1)由一次函数的定义,得: ,解得m=0或m=1,又∵m﹣1≠0即m≠1;∴当m=0时,这个函数是一次函数;
(2)由二次函数的定义,得: ,解得且,∴当且时,这个函数是二次函数.
(1)、m=0;(2)、m≠0且m≠1.
【解析】试题分析:(1)由一次函数的定义求解;
(2)由二次函数的定义求解.
试题解析:(1)由一次函数的定义,得: ,解得m=0或m=1,又∵m﹣1≠0即m≠1;∴当m=0时,这个函数是一次函数;
(2)由二次函数的定义,得: ,解得且,∴当且时,这个函数是二次函数. 已知:在△ABC中,BC=10,BC边上的高h=5,点E在边AB上,过点E作EF∥BC,交AC边于点F.点D为BC上一点,连接DE、DF.设点E到BC的距离为x,则△DEF的面积S关于x的函数图象大致为( )
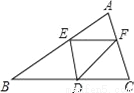
A. 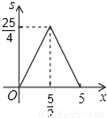 B.
B. 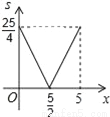 C.
C. 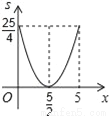 D.
D. 
 D
【解析】试题分析:∵EF∥BC,
∴△AEF∽△ABC,
∴,
∴EF=•10=10﹣2x,
∴S=(10﹣2x)•x=﹣x2+5x=﹣(x﹣)2+,
∴S与x的关系式为S=﹣(x﹣)2+(0<x<5),
纵观各选项,只有D选项图象符合.
故选D.
D
【解析】试题分析:∵EF∥BC,
∴△AEF∽△ABC,
∴,
∴EF=•10=10﹣2x,
∴S=(10﹣2x)•x=﹣x2+5x=﹣(x﹣)2+,
∴S与x的关系式为S=﹣(x﹣)2+(0<x<5),
纵观各选项,只有D选项图象符合.
故选D. 二次函数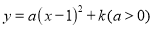 中
中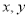 的几组对应值如下表.
的几组对应值如下表.
| -2 | 1 | 5 |
| m | n | p |
表中m、n、p的大小关系为________________(用“<”连接)
 n<m<p
【解析】【解析】
设(-2,m)关于对称轴的对称点为(x,m).∵二次函数的对称轴为x=1,∴ ,解得:x=4.∵a>0,∴抛物线开口向上,在对称轴右侧,y随x的增大而增大.∵1<4<5,∴n<m<p.故答案为:n<m<p.
n<m<p
【解析】【解析】
设(-2,m)关于对称轴的对称点为(x,m).∵二次函数的对称轴为x=1,∴ ,解得:x=4.∵a>0,∴抛物线开口向上,在对称轴右侧,y随x的增大而增大.∵1<4<5,∴n<m<p.故答案为:n<m<p. 在□ABCD中,AB=3,BC=4,则□ABCD的周长等于_______.
 14
【解析】【解析】
∵四边形ABCD是平行四边形,∴CD=AB=3,AD=BC=4,∴?ABCD的周长为14.
故答案为:14.
14
【解析】【解析】
∵四边形ABCD是平行四边形,∴CD=AB=3,AD=BC=4,∴?ABCD的周长为14.
故答案为:14.